题目内容
7.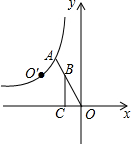 如图,点A是双曲线y=-$\frac{2}{x}$(x<0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OA}{OB}$的值为( )
如图,点A是双曲线y=-$\frac{2}{x}$(x<0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OA}{OB}$的值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
分析 过点A作AD⊥x轴于点D,由点A在反比例函数图象上设出点A的坐标,由O、A点的坐标即可得出直线OA的解析式,设出点B的坐标,由中点坐标公式以及中心对称的性质找出点O′的坐标,根据反比例函数图象上点的坐标特征即可得出点B、A横坐标之间的关系,由此即可得出结论.
解答 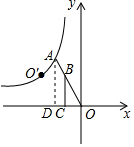 解:过点A作AD⊥x轴于点D,如图所示.
解:过点A作AD⊥x轴于点D,如图所示.
∵点A是双曲线y=-$\frac{2}{x}$(x<0)上的一点,
∴设点A的坐标为(m,-$\frac{2}{m}$),
∴直线OA的解析式为y=-$\frac{2}{{m}^{2}}$x,
设点B的坐标为(n,-$\frac{2n}{{m}^{2}}$),则点C的坐标为(n,0),
线段BC中点的坐标为(n,-$\frac{n}{{m}^{2}}$).
∵点O、O′关于点(n,-$\frac{n}{{m}^{2}}$)对称,
∴点O′的坐标为(2n,-$\frac{2n}{{m}^{2}}$).
∵点O′在反比例函数y=-$\frac{2}{x}$的图象上,
∴-$\frac{2n}{{m}^{2}}$=-$\frac{2}{2n}$,即$\frac{2{n}^{2}}{{m}^{2}}$=1,
∴$\frac{m}{n}$=$\sqrt{2}$.
∵BC⊥x轴,AD⊥x轴,
∴BC∥AD,
∴$\frac{OA}{OB}$=$\frac{m}{n}$=$\sqrt{2}$.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征、反比例函数与一次函数的交点问题已经平行线的性质,解题的关键是找出$\frac{m}{n}$=$\sqrt{2}$.本题属于中档题,难度不大,但运算稍显繁琐,解决该题型题目时,设出点的坐标,利用平行线的性质找出线段间的比例关系是关键.

练习册系列答案
相关题目
17.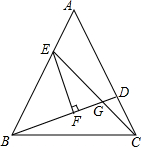 如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )
如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )
 如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )
如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 4 |
18.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=3}\\{z+x=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=3}\\{xy=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=y+11}\\{{x}^{2}-2x=y+{x}^{2}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{{x}^{2}=1}\\{y=2x}\end{array}\right.$ |
15.为了求1+2+22+23+…+22016的值,可令S=1+2+22+23+…+22016,则2S=2+22+23+24+…+22017,因此2S-S=22017-1,所以1+2+22+23+…+22016=22017-1.仿照以上推理计算出1+5+52+53+…+52016的值是( )
| A. | 52016-1 | B. | 52017-1 | C. | $\frac{{{5^{2016}}-1}}{4}$ | D. | $\frac{{{5^{2017}}-1}}{4}$ |
2.|-2|=( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 4 |
12.有下列四个命题:①相等的角是对顶角;②同位角相等;③若一个角的两边与另一个角的两边互相平行,则这两个角一定相等;④从直线外一点到这条直线的垂线段,叫做点到直线的距离.其中是真命题的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.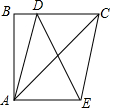 如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )
如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )
 如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )
如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
11.要使分式$\frac{x-3}{2-x}$有意义,则x的取值应满足( )
| A. | x≠3 | B. | x≠2 | C. | x<2 | D. | x>2 |