题目内容
10. 如图,点E在AC的延长线上,下列条件不能判断AC∥BD的是( )
如图,点E在AC的延长线上,下列条件不能判断AC∥BD的是( )| A. | ∠3=∠4 | B. | ∠D=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠ACD=180° |
分析 同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断即可.
解答 解:根据∠3=∠4,可得AC∥BD,故A选项能判定;
根据∠D=∠DCE,可得AC∥BD,故B选项能判定;
根据∠1=∠2,可得AB∥CD,而不能判定AC∥BD,故C选项符合题意;
根据∠D+∠ACD=180°,可得AC∥BD,故D选项能判定;
故选:C.
点评 本题主要考查了平行线的判定,解题时注意:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
相关题目
20.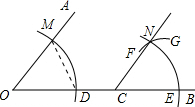 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )| A. | 线段OD的长 | B. | 线段OM的长 | C. | 线段DM的长 | D. | 线段CE的长 |
1.下列算式可用平方差公式计算的是( )
| A. | (3m-n)(-3m+n) | B. | (-a+b)(-a-b) | C. | (-a-b)(a+b) | D. | (2a+b)(2b-a) |
18.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=3}\\{z+x=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=3}\\{xy=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=y+11}\\{{x}^{2}-2x=y+{x}^{2}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{{x}^{2}=1}\\{y=2x}\end{array}\right.$ |
15.为了求1+2+22+23+…+22016的值,可令S=1+2+22+23+…+22016,则2S=2+22+23+24+…+22017,因此2S-S=22017-1,所以1+2+22+23+…+22016=22017-1.仿照以上推理计算出1+5+52+53+…+52016的值是( )
| A. | 52016-1 | B. | 52017-1 | C. | $\frac{{{5^{2016}}-1}}{4}$ | D. | $\frac{{{5^{2017}}-1}}{4}$ |
2.|-2|=( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 4 |
19.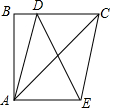 如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )
如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )
 如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )
如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,点D在BC上,以AC为对角线的所有?ADCE中DE的最小值是( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |




 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是②③.
小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是②③.