题目内容
15．计算：（1）（-5a2b）（2ab2c）；
（2）（-$\frac{3}{4}$ax）（-$\frac{2}{3}$bx2）；
（3）（2×104）（6×105）
（4）（$\frac{1}{2}$x）•2x3（-3x2）
分析 根据单项式与单项式相乘，把他们的系数分别相乘，相同字母的幂分别相加，其余字母连同他的指数不变，作为积的因式，依此分别计算即可．
解答 解：（1）（-5a2b）（2ab2c）=-10a3b3c；
（2）（-$\frac{3}{4}$ax）（-$\frac{2}{3}$bx2）=$\frac{1}{2}$abx3；
（3）（2×104）（6×105）=12×109）=1.2×1010；
（4）（$\frac{1}{2}$x）•2x3（-3x2）=-3x6．
点评 本题考查了单项式与单项式相乘，熟练掌握运算法则是解题的关键．
练习册系列答案
相关题目
如图，已知BD，CE分别为∠ABC，∠ACB的平分线，AM⊥CE于M，AN⊥BD于N．求证：MN=$\frac{1}{2}$（AB+AC-BC）．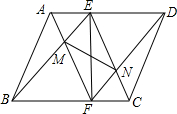
如图，在?ABCD中，点E在AD上，连BE，DF∥BE交BC于点F，AF与BE交于点M，CE与DF交于点N．求证：EF与MN互相平分．
如图，△ABC中，∠ABC=90°，以AB为直径作⊙O交AC于点D，过D作⊙O的切线交BC于点E．
如图是两块完全一样的含30°角的三角板，分别记作△ABC和△A1B1C1，现将两块三角板重叠在一起，高较长直角边的中点为M，绕中点M转动上面的三角板ABC，直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上．当∠A=30°，B1C=2时，则此时AB的长为（ ）
12．
在矩形ABCD中，BC=4，BG与对角线AC垂直且分别交AC，AD及射线CD于点E，F，G，当点F为AD中点时，∠ECF的正切值是（ ）
在矩形ABCD中，BC=4，BG与对角线AC垂直且分别交AC，AD及射线CD于点E，F，G，当点F为AD中点时，∠ECF的正切值是（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{2}}}{4}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |