题目内容
1.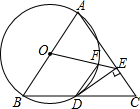 如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.(1)求证:DE是⊙O的切线;
(2)连接OE交⊙O于F,连接DF,若tan∠EDF=$\frac{1}{2}$,求cos∠DEF的值.
分析 (1)先根据圆周角定理由AB为直径得到AD⊥BC,而AB=AC,根据等腰三角形的性质得BD=CD,于是可判断OD为△ABC的中位线,根据三角形中位线的性质有OD∥AC,由于DE⊥AC,所以DE⊥OD,于是根据切线的判定定理可得到DE是⊙O的切线;
(2)根据弦切角定理得到∠EDF=$\frac{1}{2}$∠DOE,求得cos∠DOE=cos2∠EDF=1-2sin2∠EDF,根据已知条件得到sin∠EDF=$\frac{\sqrt{5}}{5}$,即可得到结论.
解答 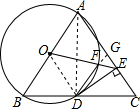 解:(1)连结OD,如图,
解:(1)连结OD,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)∵∠EDF=$\frac{1}{2}$∠DOE,
∴cos∠DOE=cos2∠EDF=1-2sin2∠EDF
,∵tan∠EDF=$\frac{1}{2}$,
∴sin∠EDF=$\frac{\sqrt{5}}{5}$,
∴cos∠DOE=$\frac{3}{5}$,
∴cos∠DEF=sin∠DOE=$\sqrt{1-(\frac{3}{5})^{2}}$=$\frac{4}{5}$.
点评 本题考查了切线的判定和性质,三角形的中位线的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
12.若分式$\frac{1}{{{x^2}+2x+m}}$无论x取何实数总有意义,则函数y=(m+1)x+(m-1)的图象经过第( )象限.
| A. | 一、二、三 | B. | 一、三、四 | C. | 二、三、四, | D. | 一、二、四 |
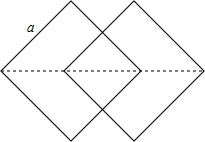 如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案.
如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案.