题目内容
12.若分式$\frac{1}{{{x^2}+2x+m}}$无论x取何实数总有意义,则函数y=(m+1)x+(m-1)的图象经过第( )象限.| A. | 一、二、三 | B. | 一、三、四 | C. | 二、三、四, | D. | 一、二、四 |
分析 首先根据分式有意义的条件确定m的取值范围,从而根据一次函数的性质确定其经过的象限.
解答 解:∵若分式$\frac{1}{{{x^2}+2x+m}}$无论x取何实数总有意义,
∴x2+2x+m≠0
∴x2+2x+1+m-1≠0,
∴(x+1)2+(m-1)≠0,
∵(x-1)2≥0,
∴m-1>0,
∴∴m>1时,分式$\frac{1}{{{x^2}+2x+m}}$无论x取何实数总有意义,
∴m+1>0,m-1>0,
∴函数y=(m+1)x+(m-1)的图象经过第一、二、三象限,
故选A.
点评 考查了一次函数图象与系数的关系及分式有意义的条件,解题的关键是根据分式有意义的条件确定m的取值范围,难度不大.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
3.若式子|x|=(x-1)0成立,则x的取值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 不存在 |
17.如图中,∠1与∠2是对顶角的是( )
| A. |  | B. | 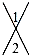 | C. | 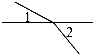 | D. | 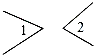 |
 已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度. 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为24cm2,求△BEF的面积.
如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为24cm2,求△BEF的面积. 如图,在菱形ABCD中,对角线AC=10,BD=24,
如图,在菱形ABCD中,对角线AC=10,BD=24,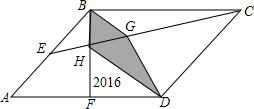 如图,平行四边形ABCD中,E、F分别为AB、AD的中点,连接BF、CE交于点H,连接HD,过B点作BG平行HD,已知△HFD的面积是2016平方厘米,求阴影四边形BGDH的面积?
如图,平行四边形ABCD中,E、F分别为AB、AD的中点,连接BF、CE交于点H,连接HD,过B点作BG平行HD,已知△HFD的面积是2016平方厘米,求阴影四边形BGDH的面积?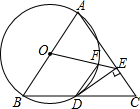 如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.