题目内容
14.设a<-1,0≤x≤-a-1,且函数y=x2+ax的最小值为-$\frac{1}{2}$,则常数a=-$\frac{3}{2}$或-2$\sqrt{2}$.分析 根据已知条件得到抛物线y=x2+ax与x轴的交点为(0,0),(-a,0),求得-a>1,抛物线y=x2+ax的对称轴为直线x=-$\frac{a}{2}$,当-$\frac{a}{2}$>1时,求得a=-$\frac{3}{2}$;当-$\frac{a}{2}$<1时,求得a=-2$\sqrt{2}$.
解答 解:令y=0,则x2+ax=0,
解得:x=0或-a,
∴抛物线y=x2+ax与x轴的交点为(0,0),(-a,0),
∵a<-1,
∴-a>1,
∵抛物线y=x2+ax的对称轴为直线x=-$\frac{a}{2}$,
∴当-$\frac{a}{2}$>1时,
即当x=1时,函数y=x2+ax有最小值,
∴1+a=-$\frac{1}{2}$,
∴a=-$\frac{3}{2}$;
当-$\frac{a}{2}$<1时,
即当x=-$\frac{a}{2}$时,函数y=x2+ax有最小值,
∴-$\frac{{a}^{2}}{4}$=-$\frac{1}{2}$,
∴a=±2$\sqrt{2}$;
∵a<-1,
∴a=-2$\sqrt{2}$,
综上所述:常数a=-$\frac{3}{2}$或-2$\sqrt{2}$,
故答案为:-$\frac{3}{2}$或-2$\sqrt{2}$.
点评 本题主要考查二次函数的最值,掌握二次函数的单调性是解题的关键,注意分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列命题中,假命题是( )
| A. | 矩形的对角线相等 | |
| B. | 菱形的面积等于两条对角线乘积的一半 | |
| C. | 对角线互相垂直的矩形是正方形 | |
| D. | 有两个角相等的梯形是等腰梯形 |
2.有3张边长为a的正方形纸片,4张边长分别为a、b(b<a)的长方形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )
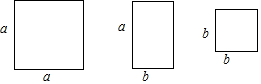

| A. | a+b | B. | 2a+b | C. | 2a-b | D. | a+2b |
6. 如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )| A. | 18° | B. | 29° | C. | 58° | D. | 38° |
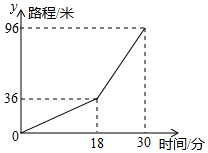 小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.
小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.