题目内容
2.有3张边长为a的正方形纸片,4张边长分别为a、b(b<a)的长方形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )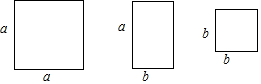
| A. | a+b | B. | 2a+b | C. | 2a-b | D. | a+2b |
分析 根据3张边长为a的正方形纸片的面积是3a2,4张边长分别为a、b(b>a)的矩形纸片的面积是4ab,5张边长为b的正方形纸片的面积是5b2,得出a2+4ab+4b2=(a+2b)2,再根据正方形的面积公式即可得出答案.
解答 解:3张边长为a的正方形纸片的面积是3a2,
4张边长分别为a、b(b>a)的矩形纸片的面积是4ab,
5张边长为b的正方形纸片的面积是5b2,
∵a2+4ab+4b2=(a+2b)2,
∴拼成的正方形的边长最长可以为(a+2b),
故选D.
点评 此题考查了完全平方公式的几何背景,关键是根据题意得出a2+4ab+4b2=(a+2b)2,用到的知识点是完全平方公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列图形中,不是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 正八边形 | D. | 等边三角形 |
7.下列根式中:$\sqrt{2a}$,$\sqrt{1+a}$,$\sqrt{{a}^{2}+{b}^{2}}$,$\sqrt{{n}^{2}+2n+1}$,$\sqrt{10}$,$\sqrt{12}$,是最简二次根式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.一元二次方程x2=1的解是( )
| A. | x=1 | B. | x=-1 | C. | x1=1,x2=-1 | D. | x=0 |
 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.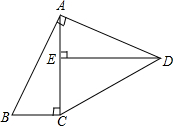 如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.
如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.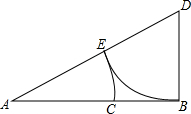 如图,线段AB=2,过点B作BD⊥AB,使BD=$\frac{1}{2}$AB,连接AD,在AD上截取DE=DB.在AB上截取AC=AE.那么线段AC的长为$\sqrt{5}$-1.
如图,线段AB=2,过点B作BD⊥AB,使BD=$\frac{1}{2}$AB,连接AD,在AD上截取DE=DB.在AB上截取AC=AE.那么线段AC的长为$\sqrt{5}$-1.