题目内容
3.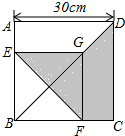 如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.
如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.
分析 根据正方形的性质可证△OEG≌△OBF,由此可知S阴影=$\frac{1}{2}$S正方形ABCD.
解答 解:设小正方形EBFG的对角线相交于点O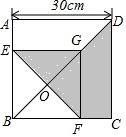
∵在正方形EBFG中,对角线EF与BG互相垂直平分,
∴在△OEG与△OBF中,$\left\{\begin{array}{l}{OE=OB}\\{∠EOG=∠BOF=90°}\\{OG=OF}\end{array}\right.$
∴△OEG≌△OBF
∴S阴影=$\frac{1}{2}$S正方形ABCD=$\frac{1}{2}$×30×30=450(cm2)
即阴影部分的面积为450cm2.
故答案为:450cm2
点评 本题考查了正方形的性质、全等三角形的判定与性质等知识点,解题的关键是证明S阴影=$\frac{1}{2}$S正方形ABCD

练习册系列答案
相关题目
14.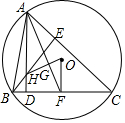 如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
 如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )| A. | 2:4 | B. | 1:3 | C. | 2:5 | D. | 1:4 |
18.当x=$\sqrt{3}$时,代数式$\sqrt{(x-2)^{2}}$+$\root{3}{(1-x)^{3}}$的值是( )
| A. | 3 | B. | 1-2$\sqrt{3}$ | C. | 3-2$\sqrt{3}$ | D. | 2$\sqrt{3}$-1 |
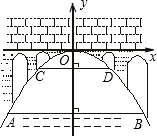 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m. 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA. 如图,已知长方形的长为a,宽为2,两个半圆的直径都为2,用含a的式子表示出阴影部分的面积.
如图,已知长方形的长为a,宽为2,两个半圆的直径都为2,用含a的式子表示出阴影部分的面积.