题目内容
5.观察下列等式:①$\frac{1}{1×2}$=1-$\frac{1}{2}$,②$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,③$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$.
将以上三个等式两边分别相加,得
$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$.
(1)请写出第④个式子$\frac{1}{4×5}$=$\frac{1}{4}-\frac{1}{5}$
(2)猜想并写出:$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
(3)探究并计算:$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{100×102}$.
分析 (1)规律:相邻的两个数的积的倒数等于它们的倒数的差,故第四个式子为:$\frac{1}{4×5}$=$\frac{1}{4}-\frac{1}{5}$
(2)根据以上规律直接写出即可.
(3)各项提出$\frac{1}{2}$之后即可应用(1)中的方法进行计算.
解答 解:(1)答案为:$\frac{1}{4×5}$=$\frac{1}{4}-\frac{1}{5}$
(2)答案为:$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
(3)$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{100×102}$
=$\frac{1}{4}$×($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{50×51}$)
=$\frac{1}{4}$×$\frac{50}{51}$
=$\frac{25}{102}$
点评 本题考查了数字的变化规律问题,解题的关键是总结出数字变化的规律并加以运用.

练习册系列答案
相关题目
4.解方程求出两个根x1、x2,并计算两个根的和与积,完成下表.
(1)补全上述表格;
(2)观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律?写出你的结论;(用文字或式子表达)
(3)根据表格中所得的规律解答:已知x1,x2是方程3x2-4x-2=0的两根,求x12+x22的值.
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| 9x2-2=0 | $\frac{\sqrt{2}}{3}$ | -$\frac{\sqrt{2}}{3}$ | 0 | |
| 2x2-3x=0 | 0 | $\frac{3}{2}$ | $\frac{3}{2}$ | 0 |
| x2-3x+2=0 | 1 | 2 | 3 | 2 |
| 关于x的方程ax2+bx+c=0(a≠0,b2-4ac≥0) | $\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$ | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ |
(2)观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律?写出你的结论;(用文字或式子表达)
(3)根据表格中所得的规律解答:已知x1,x2是方程3x2-4x-2=0的两根,求x12+x22的值.
14.刘亮的妈妈每天早上要送新鲜蔬菜到市场去卖,下面是一周送出的20筐新鲜蔬菜的质量记录(每筐以25kg为标准质量,单位:kg)
求一周送出20筐新鲜蔬菜的总重量.
| 筐 数 | 2 | 5 | 3 | 4 | 2 | 4 |
| 与标准质量比较 | -0.8 | +0.6 | -0.5 | +0.4 | +0.5 | -0.3 |
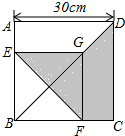 如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.
如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.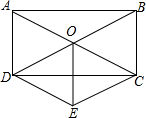 如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.
如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.