题目内容
9.观察下列各式:①1×3=12+2×1;②2×4=22+2×2;③3×5=32+2×3;…则第n个式子可以表示为n×(n+2)=n2+2n.分析 根据所给的3个算式:①1×3=12+2×1;②2×4=22+2×2;③3×5=32+2×3;可得:第n个式子左边的两个因数分别是n、n+2,第n个式子右边是n2与2n的和,据此判断出第n个式子可以表示为多少即可.
解答 解:观察下列各式:①1×3=12+2×1;②2×4=22+2×2;③3×5=32+2×3;…
则第n个式子可以表示为n×(n+2)=n2+2n.
故答案为:n×(n+2)=n2+2n.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律.

练习册系列答案
相关题目
19.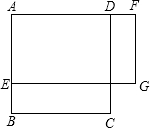 如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
 如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )| A. | y=5-x | B. | y=5-x2 | C. | y=25-x | D. | y=25-x2 |
20. 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-2 |
1.在△ABC中,∠C=90°,tanA=$\frac{12}{5}$,△ABC的周长为60,那么△ABC的面积为( )
| A. | 60 | B. | 30 | C. | 240 | D. | 120 |



