题目内容
17.证明:(1+$\frac{1}{n}$-$\frac{1}{n+1}$)2=1+$\frac{1}{{n}^{2}}$+$\frac{1}{(n+1)^{2}}$(n为正整数)分析 根据完全平方公式将式子展开即可证明结论成立.
解答 证明:(1+$\frac{1}{n}$-$\frac{1}{n+1}$)2
=$1+\frac{1}{n}-\frac{1}{n+1}$$+\frac{1}{n}+\frac{1}{{n}^{2}}-\frac{1}{n(n+1)}$$-\frac{1}{n+1}-\frac{1}{n(n+1)}+\frac{1}{(n+1)^{2}}$
=1+$\frac{1}{{n}^{2}}$+$\frac{1}{(n+1)^{2}}$.
点评 本题考查分式的混合运算,解答本题的关键是明确分式的混合运算的计算方法.

练习册系列答案
相关题目
5.下列字母中,属于中心对称图形的是( )
| A. | D | B. | X | C. | V | D. | R |
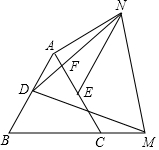 如图,等边△ABC中,AB=8,点D、E分别为AB、AC的中点,点M为射线BC上一动点,以DM为一边作等边△DMN.∠DAN=150°,DN交AE于F,线段NF的长为$\frac{2\sqrt{7}}{3}$.
如图,等边△ABC中,AB=8,点D、E分别为AB、AC的中点,点M为射线BC上一动点,以DM为一边作等边△DMN.∠DAN=150°,DN交AE于F,线段NF的长为$\frac{2\sqrt{7}}{3}$.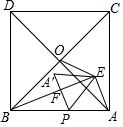 如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.
如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.