题目内容

1．在△ABC中，∠C=90°，tanA=$\frac{12}{5}$，△ABC的周长为60，那么△ABC的面积为（　　）
A．60B．30C．240D．120

分析 由tanA的值，利用锐角三角函数定义设出BC与AC，进而利用勾股定理表示出AB，由周长为60求出x的值，确定出两直角边，即可求出三角形面积．

解答 解：如图所示，由tanA=$\frac{12}{5}$，
设BC=12x，AC=5x，根据勾股定理得：AB=13x，
由题意得：12x+5x+13x=60，
解得：x=2，
∴BC=24，AC=10，
则△ABC面积为120，
故选D

点评 此题考查了解直角三角形，锐角三角函数定义，以及勾股定理，熟练掌握勾股定理是解本题的关键．

练习册系列答案
相关题目
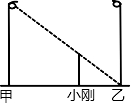11．如图，甲、乙两盏路灯相距30米，一天晚上，当小刚从路灯甲底部向路灯乙底部直行25米时，发现自己的身影顶部正好接触到路灯乙的底部，已知小刚的身高为1.5米，那么路灯甲的高为（　　）
A．9米B．8米C．7米D．6米
12．（1）比较下列各式的大小：
①|-2|+|3|与|-2+3|；
②|-2|+|-3|与|-2-3|；
③|-2|+|0|与|-2+0|；
（2）请你由（1）归纳总结出|a|+|b|与|a+b|（a、b为有理数）的大小关系，并用文字语言叙述此关系；
（3）根据（2）中的结论，求当|x|+2016=|x-2016|时，x的取值范围．
9．观察下列各式：①1×3=12+2×1；②2×4=22+2×2；③3×5=32+2×3；…则第n个式子可以表示为n×（n+2）=n2+2n．
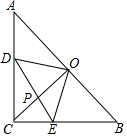16．在Rr△ABC中，∠C=90°，AC=BC=1，点O为AB的中点，点D、E分别为AC、AB边上的动点，且保持DO⊥EO，连接CO、DE交于点P．
（1）求证：OD=OE；
（2）在运动的过程中，DP•EP是否存在最大值？若存在，请求出DP•EP的最大值；若不存在，请说明理由．
（3）若CD=2CE，求DP的长度．
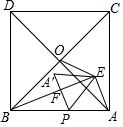6．如图，在△ABE中，∠AEB=90°，AB=$\sqrt{29}$，以AB为边在△ABE的同侧作正方形ABCDD，点O是正方形对角线的交．点，连接OE，OE=$\frac{3}{2}$$\sqrt{2}$，点P为AB上一动点，将△APE沿直线PE翻折得到△A′PE，当A′P⊥BE于点F时，BF的长度是5-$\frac{10\sqrt{29}}{29}$．
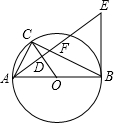13．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，经过点A作AE⊥OC，垂足为点D，AE与BC交于点F，与过点B的直线交于点E，且EB=EF．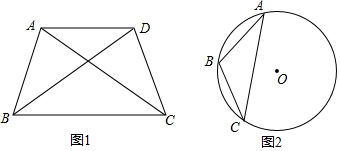
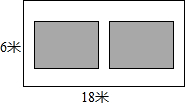（1）求证：BE是⊙O的切线；
（2）若CD=1，cos∠AEB=$\frac{3}{5}$，求BE的长．
10．若一个四边形的一条对角线把四边形分成两个等腰三角形，且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍，我们把这条对角线叫做这个四边形的黄金线，这个四边形叫做黄金四边形．
（1）如图1，在四边形ABCD中，AB=AD=DC，对角线AC，BD都是黄金线，且AB＜AC，CD＜BD，求四边形ABCD各个内角的度数；
（2）如图2，点B是弧AC的中点，请在⊙O上找出所有的点D，使四边形ABCD的对角线AC是黄金线（要求：保留作图痕迹）；
（3）在黄金四边形ABCD中，AB=BC=CD，∠BAC=30°，求∠BAD的度数．
11．如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道，则人行道的宽度为多少米？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网