题目内容
16. 如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.①求证:△ABE∽△DBC;
②求线段AE的长.
分析 (1)由等腰三角形的性质可知∠ABD=∠ADB,由AD∥BC可知,∠ADB=∠DBC,由此可得∠ABD=∠DBC,又因为∠AEB=∠C=90°,所以可证△ABE∽△DBC;
(2)由等腰三角形的性质可知,BD=2BE,根据△ABE∽△DBC,利用相似比求BE,在Rt△ABE中,利用勾股定理求AE即可.
解答 (1)证明:∵AB=AD=25,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC;
(2)解:∵AB=AD,又AE⊥BD,
∴BE=DE,
∴BD=2BE,
由△ABE∽△DBC,
得$\frac{AB}{BD}=\frac{BE}{BC}$,
∵AB=AD=25,BC=32,
∴$\frac{25}{2BE}=\frac{BE}{32}$,
∴BE=20,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=15.
点评 本题考查了相似三角形的判定与性质.关键是要懂得找相似三角形,利用相似三角形的性质及勾股定理解题.

练习册系列答案
相关题目
14.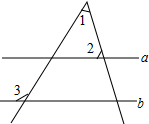 如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )
如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )
 如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )
如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )| A. | 85° | B. | 95° | C. | 105° | D. | 115° |
5.下列计算中,结果是正数的是( )
| A. | 1-3 | B. | (-1)×3 | C. | 3-1 | D. | (-1)3 |




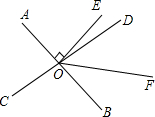 如图,直线AB与CD相交于点O,OE⊥AB,∠AOC:∠AOD=4:5,OF平分∠BOD,求∠EOF的度数.
如图,直线AB与CD相交于点O,OE⊥AB,∠AOC:∠AOD=4:5,OF平分∠BOD,求∠EOF的度数.