题目内容
8.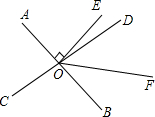 如图,直线AB与CD相交于点O,OE⊥AB,∠AOC:∠AOD=4:5,OF平分∠BOD,求∠EOF的度数.
如图,直线AB与CD相交于点O,OE⊥AB,∠AOC:∠AOD=4:5,OF平分∠BOD,求∠EOF的度数.
分析 设∠AOC=4x,则∠AOD=5x,根据邻补角的定义得到∠AOC+∠AOD=180°,即4x+5x=180°,解得x=20°,则∠AOC=4x=80°,利用对顶角相等得∠BOD=80°,由OE⊥AB得到∠BOE=90°,则∠DOE=∠BOE-∠BOD=10°,再根据角平分线的定义得到∠DOF=$\frac{1}{2}$∠BOD=40°,利用∠EOF=∠EOD+∠DOF即可得到∠EOF的度数.
解答 解:设∠AOC=4x,则∠AOD=5x,
∵∠AOC+∠AOD=180°,
∴4x+5x=180°,解得x=20°,
∴∠AOC=4x=80°,
∴∠BOD=80°,
∵OE⊥AB,
∴∠BOE=90°,
∴∠DOE=∠BOE-∠BOD=10°,
又∵OF平分∠DOB,
∴∠DOF=$\frac{1}{2}$∠BOD=40°,
∴∠EOF=∠EOD+∠DOF=10°+40°=50°.
点评 本题考查了垂线的性质:两直线垂直,则它们相交所成的角为90°.也考查了对顶角相等以及邻补角的定义,以及方程思想的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.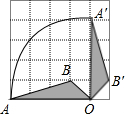 如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )
如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )
 如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )
如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |
20.下列计算结果为负数的是( )
| A. | |-3| | B. | (-3)0 | C. | -(+3) | D. | (-3)2 |
 如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E. 如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.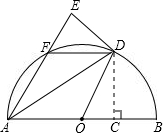 如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD翻折得到△AED,AE交半圆O于点F,连接DF、OD.
如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD翻折得到△AED,AE交半圆O于点F,连接DF、OD.