题目内容
1．在同一平面直角坐标系中，函数y=ax2+bx（a≠0）与y=bx+a（b≠0）的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据各个选项中的函数图象可以判断函数y=ax2+bx（a≠0）与y=bx+a（b≠0）中a、b的正负，从而可以得到哪个选项是正确的．
解答 解：在A中，由一次函数图象可知，a＞0，b＞0，由二次函数图象可知，a＞0，b＜0，故选项A错误；
在B中，由一次函数图象可知，a＜0，b＜0，由二次函数图象可知，a＞0，b＞0，故选项B错误；
在C中，由一次函数图象可知，a＜0，b＞0，由二次函数图象可知，a＜0，b＞0，故选项C正确；
在D中，由一次函数图象可知，a＞0，b＞0，由二次函数图象可知，a＜0，b＜0，故选项D错误；
故选C．
点评 本题考查二次函数的图象，解题的关键是明确函数图象与a、b的关系，注意一次函数y=bx+a（b≠0）中，b是一次项系数．
练习册系列答案
相关题目
19．在“六城”同创活动中，为努力把我市建成“国家园林城市”，绿化公司计划购买A、B、C三种绿化树共800株，用20辆货车一次运回，对我市城区新建道路进行绿化．按计划，20辆货车都要装运，每辆货车只能装运同一种绿化树，且必须装满．根据下表提供的信息，解答以下问题：
（1）设装运A种绿化树的车辆数为x，装运B种绿化树的车辆数为y，求y与x之间的函数关系式；
（2）如果装运每种绿化树的车辆数都不多于8辆，那么车辆的安排方案有几种？并写出每种安排方案；
（3）若在“六城”同创活动中要求“厉行节约”办实事，则应采用（2）中的哪种安排方案？为什么？
| 绿 化 树 品 种 | A | B | C |
| 每辆货车运载量（株） | 40 | 48 | 32 |
| 每株树苗的价格（元） | 20 | 50 | 30 |
（2）如果装运每种绿化树的车辆数都不多于8辆，那么车辆的安排方案有几种？并写出每种安排方案；
（3）若在“六城”同创活动中要求“厉行节约”办实事，则应采用（2）中的哪种安排方案？为什么？
9．如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题
（1）将下面的表格补充完整：
（2）根据规律，是否存在一个正多边形，其中的∠α=20°？若存在，请求出n的值，若不存在，请说明理由．
（1）将下面的表格补充完整：
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| ∠α的度数 | 60° | 45° | 36° | 30° | … | （$\frac{180}{n}$）° |
如图，在四边形ABCD中，AD∥BC，∠C=90°，AB=AD=25，BC=32，连接BD，AE⊥BD，垂足为E．
6．点A在平面直角坐标系中的第四象限，且点A到x轴的距离为1，到y轴的距离为3，则A的坐标为（ ）
| A． | （-3，1） | B． | （3，-1） | C． | （-1，3） | D． | （1，-3） |
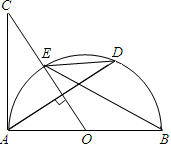如图，AB是⊙O的直径，过圆心O作弦AD的垂线交半⊙O于点E，交AC于点C，使∠BED=∠C．