题目内容
4.如图①所示的正三角形纸板的边长为1,周长记为P1,沿图①的底边剪去一块边长为$\frac{1}{2}$的正三角形纸板后得到图②,然后沿同一底边一次剪去一块更小的正三角板(即其边长为前一块被减掉正三角形纸板边长的$\frac{1}{2}$)后,得图③,图④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=${(\frac{1}{2})}^{n-1}$(用含n的代数式表示)
分析 利用等边三角形的性质(三边相等)求出等边三角形的周长P1,P2,P3,P4,根据周长相减的结果能找到规律即可求出答案.
解答 解:∵P1=1+1+1=3,
P2=1+1+$\frac{1}{2}$=$\frac{5}{2}$,
P3=1+1+$\frac{1}{4}$×3=$\frac{11}{4}$,
P4=1+1+$\frac{1}{4}$×2+$\frac{1}{8}$×3=$\frac{23}{8}$,
…
∴p3-p2=$\frac{11}{4}$-$\frac{5}{2}$=$\frac{1}{4}$=($\frac{1}{2}$)2;
P4-P3=$\frac{23}{8}$-$\frac{11}{4}$=$\frac{1}{8}$=($\frac{1}{2}$)3,
…
则Pn-Pn-1=($\frac{1}{2}$)n-1.
故答案为:${(\frac{1}{2})}^{n-1}$.
点评 此题考查图形的变化规律,解答此题的关键是通过观察图形,分析、归纳发现其中的运算规律,并应用规律解决问题.

练习册系列答案
相关题目
14.下列长度的三根木棒首尾相接,能做成三角形框架的是( )
| A. | 1cm、2cm、3cm | B. | 2cm、3cm、4cm | C. | 4cm、9cm、4cm | D. | 2cm、1cm、4cm |
15. 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )
 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )| A. | 3$\sqrt{2}$-4 | B. | 3$\sqrt{2}$-3 | C. | 3$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-1 |
 这是一根起点为0的数轴,现有同学将它弯折,如图所示,例如:虚线上第一行0,第二行6,第三行21…,第10行的数是378.
这是一根起点为0的数轴,现有同学将它弯折,如图所示,例如:虚线上第一行0,第二行6,第三行21…,第10行的数是378. 如图,在△ABC中,∠ABC=56°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠ABE=28度.
如图,在△ABC中,∠ABC=56°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠ABE=28度.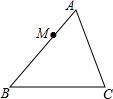 如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=4或6.
如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=4或6.