题目内容
 已知弦AB、CD相交于E,
已知弦AB、CD相交于E, |
| AC |
 |
| BD |
考点:圆周角定理
专题:
分析:首先连接BC,根据圆周角定理可得∠ABC=45°,∠BCD=15°,再根据三角形外角的性质即可求得.
解答: 解:连接BC,
解:连接BC,
∵
的度数为90°,
的度数为30°,
∴∠ABC=45°,∠BCD=15°,
∴∠AEC=∠ABC+∠BCD=60°.
故答案为60°.
 解:连接BC,
解:连接BC,∵
 |
| AC |
 |
| BD |
∴∠ABC=45°,∠BCD=15°,
∴∠AEC=∠ABC+∠BCD=60°.
故答案为60°.
点评:此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,函数y=-﹙x-1﹚2+c的图象与x轴的一个交点坐标为(3,0),则另一交点的横坐标为( )
如图,函数y=-﹙x-1﹚2+c的图象与x轴的一个交点坐标为(3,0),则另一交点的横坐标为( )| A、-4 | B、-3 | C、-2 | D、-1 |
 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结DE.若AB=8,CD=2,则DE的长为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结DE.若AB=8,CD=2,则DE的长为( )A、4
| ||
B、5
| ||
C、4
| ||
D、3
|
关于y的方程3y+5=0与3y+3k=1的解完全相同,则k的值为( )
| A、-2 | ||
B、
| ||
| C、2 | ||
D、-
|
 如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P.
如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P. 已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,还要添加的条件为
已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,还要添加的条件为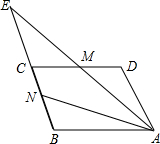 如图,已知M、N分别是平行四边形ABCD边DC、BC的中点,射线AM和射线BC相交于E,设
如图,已知M、N分别是平行四边形ABCD边DC、BC的中点,射线AM和射线BC相交于E,设 如图,ABCD是一个长方形盒子的正面,小明想知道AB边与CD边是否垂直于BC边,他利用随身带的卷尺量得AB=5cm,BC=12cm,A、C两点的距离是13cm.由此,小明判断出AB边垂直于BC边.你知道这是为什么吗?
如图,ABCD是一个长方形盒子的正面,小明想知道AB边与CD边是否垂直于BC边,他利用随身带的卷尺量得AB=5cm,BC=12cm,A、C两点的距离是13cm.由此,小明判断出AB边垂直于BC边.你知道这是为什么吗?