题目内容
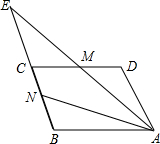如图，已知M、N分别是平行四边形ABCD边DC、BC的中点，射线AM和射线BC相交于E，设| AB |
| a |
| AD |
| b |
| a |
| b |
| AN |
| AE |
考点：*平面向量
专题：
分析：由四边形ABCD是平行四边形，可得
=
=
，
=
=
，又由M、N分别是平行四边形ABCD边DC、BC的中点，即可得
=
=
，
=
=
，然后由三角形法则求得
与
的值，再由△ECM∽△EBA，根据相似三角形的对应边成比例，即可求得答案．
| BC |
| AD |
| b |
| DC |
| AB |
| a |
| BN |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| b |
| DM |
| 1 |
| 2 |
| DC |
| 1 |
| 2 |
| a |
| AN |
| AM |
解答：解：四边形ABCD是平行四边形，
∴
=
=
，
=
=
，
∵M、N分别是平行四边形ABCD边DC、BC的中点，
∴
=
=
，
=
=
，
∴
=
+
=
+
，
=
+
=
+
，
∵AB∥CD，M是CD中点，
∴△ECM∽△EBA，CM=
CD=
AB，
∴EM：EA=CM：AB=1：2，
∴
=2
=
+2
．
∴
| BC |
| AD |
| b |
| DC |
| AB |
| a |
∵M、N分别是平行四边形ABCD边DC、BC的中点，
∴
| BN |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| b |
| DM |
| 1 |
| 2 |
| DC |
| 1 |
| 2 |
| a |
∴
| AN |
| AB |
| BN |
| a |
| 1 |
| 2 |
| b |
| AM |
| AD |
| DM |
| b |
| 1 |
| 2 |
| a |
∵AB∥CD，M是CD中点，
∴△ECM∽△EBA，CM=
| 1 |
| 2 |
| 1 |
| 2 |
∴EM：EA=CM：AB=1：2，
∴
| AE |
| AM |
| a |
| b |
点评：本题考查了平面向量及平行四边形的性质，解答本题注意利用平行线分线段成比例的知识，难度一般．
练习册系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
如图，在⊙O中，半径OA⊥弦BC，点E为垂足，点D在优弧上．下列命题中正确的命题有（ ）
①经过线段中点的直线只有一条
②线段上任一点到垂直平分线两端距离相等；
③线段垂直平分线上任一点到线段两端距离相等；
④点P在线段AB外且PA=PB，过P作直线MN，则MN是线段AB的垂直平分线；
⑤过线段上任一点可以作这条线段的中垂线．
①经过线段中点的直线只有一条
②线段上任一点到垂直平分线两端距离相等；
③线段垂直平分线上任一点到线段两端距离相等；
④点P在线段AB外且PA=PB，过P作直线MN，则MN是线段AB的垂直平分线；
⑤过线段上任一点可以作这条线段的中垂线．
| A、①② | B、③ | C、⑤ | D、②⑤ |
一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度是（ ）
| A、第一次右拐60°，第二次左拐120° |
| B、第一次左拐60°，第二次右60° |
| C、第一次左拐60°，第二次左拐120° |
| D、第一次右拐60°，第二次右拐60° |
如图，△ABC中，BC=10，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G．求△AEG的周长．
已知弦AB、CD相交于E，
已知CD∥AE，∠1=∠2，∠3=∠4，判断△ABC是否是直角三角形，说明理由．
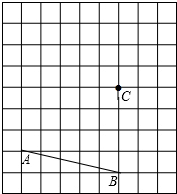画图题：