题目内容
三棱柱有 个面 个顶点 条棱，四棱柱有 个面 个顶点 条棱，五棱柱有 个面 个顶点 条棱，…，由此可以推测n棱柱有 个面， 个顶点， 条棱．
考点：认识立体图形
专题：
分析：由于三棱柱有5个面、6个顶点、9条棱，四棱柱有6个面、8个顶点、12条棱，五棱柱有7个面、10个顶点、15条棱，即棱柱的面数比棱柱数多2，顶点个数是棱柱数的2倍，棱的条数是棱数的3倍，由此可得到n棱柱的面数、顶点数和棱的条数．
解答：解：三棱柱有5个面6个顶点9条棱，四棱柱有6个面 8个顶点12条棱，五棱柱有 7个面10个顶点 15条棱，…，由此可以推测n棱柱有n+2个面，2n个顶点，3n条棱．
故答案为：5，6，9，6，8，12，7，10，15，n+2，2n，3n．
故答案为：5，6，9，6，8，12，7，10，15，n+2，2n，3n．
点评：本题考查了认识立体图形：结合实物，认识常见的立体图形，如：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等．
练习册系列答案
相关题目
如图是一个由多个正方体搭成的几何体俯视图，图中所示数字为该小正方体的个数，则这个几何体的左视图为（ ）
已知弦AB、CD相交于E，
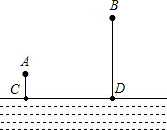如图，A、B两个化工厂在河道CD的同侧，A、B两厂到河的距离分别为AC=2km，BD=3km，CD=12km，现在河边CD上建污水处理站，将A、B两厂输送的污水处理后再排入河道，设铺设排污水管的费用为20000元/千米，请你在河道CD边上选择污水站位置O，使铺设排污水管的费用最省，并求出铺设排污水管的总费用？
已知CD∥AE，∠1=∠2，∠3=∠4，判断△ABC是否是直角三角形，说明理由．
已知函数y1=ax2与函数y2=x+
如图，直线y=某音乐会共有200名听众，参加音乐会的听众都有买票，成人票每张50元，学生票每张20元，此次音乐会的售票收入为5770元，问这场音乐会成人票、学生票各卖了多少张？设成人票有x张，列方程为（ ）
| A、50x+20x=5770 |
| B、50x+20（200-x）=5770 |
| C、50（200-x）+20x=5770 |
| D、20（200+x）+50x=5770 |