题目内容
11.解方程x2+6x+1=0.分析 配方法求解可得.
解答 解:∵x2+6x=-1,
∴x2+6x+9=-1+9,即(x+3)2=8,
∴x+3=±2$\sqrt{2}$,
则x=-3±2$\sqrt{2}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
2.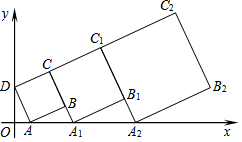 在平面直角坐标系中,正方形ABCD的位置如下图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2012个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如下图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2012个正方形的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如下图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2012个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如下图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2012个正方形的面积为( )| A. | $\sqrt{10}$×($\frac{4}{3}$)4022 | B. | 10×($\frac{4}{3}$)4022 | C. | 5×($\frac{4}{3}$)4022 | D. | 10×($\frac{4}{3}$)4023 |
19.如图1,在边长为4的正△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5.5秒时,PD的长是( )
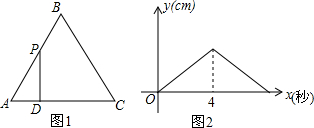

| A. | $\frac{5\sqrt{3}}{4}$cm | B. | $\frac{5\sqrt{3}}{2}$cm | C. | 2$\sqrt{3}$cm | D. | 3$\sqrt{3}$cm |
6.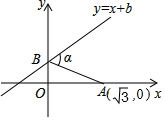 如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
 如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )| A. | 3$\sqrt{3}$-3 | B. | $\sqrt{3}$+3 | C. | 2$\sqrt{3}$+3 | D. | 2$\sqrt{3}$-3 |
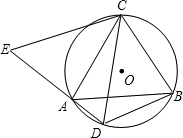 如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.
如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.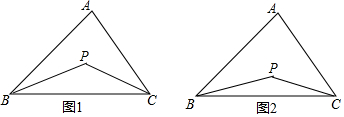 【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?
【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?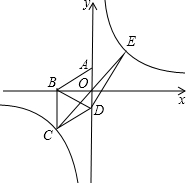 如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.
如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.