题目内容
11．观察下列各式及展开式：（a+b）2=a2+2ab+b2，（a+b）3=a3+3a2b+3ab2+b3，（a+b）4=a4+4a3b+6a2b2+4ab3+b4，（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5，…，则（a+b）n（n≥2）的展开式第三项的系数是$\frac{n（n+1）}{2}$．分析 根据各式与展开式系数规律，确定出所求展开式第三项系数即可．
解答 解：当n=2、3、4、…时，（a+b）n展开式的第三项系数分别为$\frac{2×（2-1）}{2}$=1、$\frac{3×（3-1）}={2}$3、$\frac{4×（4-1）}={2}$6、…，
则（a+b）n展开式的第三项系数为$\frac{n（n+1）}{2}$．
故答案为：$\frac{n（n+1）}{2}$．
点评 此题考查了完全平方公式，弄清题中的规律是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知：如图，BE⊥DE，∠1=∠B，∠2=∠D，试确定AB与CD的位置关系，并说明理由．
19．
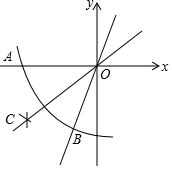如图，在平面直角坐标系中，依下列步骤尺规作图，并保留作图痕迹：
步骤1：以点O为圆心，任意长为半径画弧，与x轴负半轴交于点A，与直线y=$\sqrt{3}$x交于点B（点B在第三象限）：
步骤2：分别以点A，B为圆心，以大于$\frac{1}{2}$AB长为半径画弧，两弧交于点C．
则直线OC的函数解析式为（ ）
如图，在平面直角坐标系中，依下列步骤尺规作图，并保留作图痕迹：步骤1：以点O为圆心，任意长为半径画弧，与x轴负半轴交于点A，与直线y=$\sqrt{3}$x交于点B（点B在第三象限）：
步骤2：分别以点A，B为圆心，以大于$\frac{1}{2}$AB长为半径画弧，两弧交于点C．
则直线OC的函数解析式为（ ）
| A． | y=$\frac{\sqrt{3}}{2}$x | B． | y=-$\frac{\sqrt{3}}{2}$x | C． | y=$\frac{\sqrt{3}}{3}$x | D． | y=-$\frac{\sqrt{3}}{3}$x |
6．
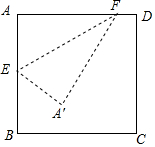如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（ ）
如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{π}{4}$ | C． | $\sqrt{2}$-1 | D． | $\frac{π}{2}$-1 |
16．
如图，已知点C在线段AB上，点C所表示的数为m，则-m不可能是（ ）
如图，已知点C在线段AB上，点C所表示的数为m，则-m不可能是（ ）| A． | 2 | B． | $\frac{3}{2}$ | C． | -1 | D． | -3 |
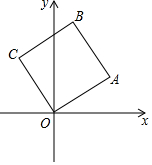已知直角坐标系中边长为1的正方形OABC，A、B，两点在第一象限．OA与x轴的角为30°，那么点B的坐标是（$\frac{\sqrt{3}-1}{2}$，$\frac{\sqrt{3}+1}{2}$）．