题目内容
7. 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{5}{13}$.
如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{5}{13}$.
分析 由在4×4正方形网格中,任选取一个白色的小正方形并涂黑,共有13种等可能的结果,使图中黑色部分的图形构成一个轴对称图形的有5种情况,直接利用概率公式求解即可求得答案.
解答 解:如图,
∵根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,白色的小正方形有13个,而能构成一个轴对称图形的有5个情况,
∴使图中黑色部诶的图形仍然构成一个轴对称图形的概率是:$\frac{5}{13}$.
故答案为:$\frac{5}{13}$.
点评 本题考查的是概率公式,熟记随机事件A的概率P(A)=事件A可能出现的结果数所有可能出现的结果数的商是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
15.在平面直角坐标系中,⊙O的半径为5,圆心在原点O,则P(-3,4)与⊙O的位置关系是( )
| A. | 在⊙O上 | B. | 在⊙O内 | C. | 在⊙O外 | D. | 不能确定 |
2. 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
16.顺次连接对角线相等的四边形各边中点,所形成的四边形是( )
| A. | 梯形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
17.如果关于x的一元二次方程x2-2x+m=0有实数根,那么m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
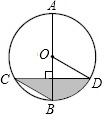 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=$\frac{8π}{3}$.
如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=$\frac{8π}{3}$.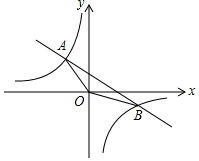 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{n}{x}$的图象相交于A(-1,2),B(2,m)两点,连接OA,OB.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{n}{x}$的图象相交于A(-1,2),B(2,m)两点,连接OA,OB.