题目内容
12.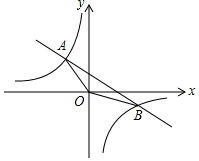 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{n}{x}$的图象相交于A(-1,2),B(2,m)两点,连接OA,OB.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{n}{x}$的图象相交于A(-1,2),B(2,m)两点,连接OA,OB.(1)分别求这两个函数的表达式;
(2)直接写出使得一次函数y=kx+b的值大于反比例函数y=$\frac{n}{x}$的值的x的取值范围,并求出△OAB的面积.
分析 (1)先把A(-1,2)代入反比例函数y=$\frac{n}{x}$求出n的值即可得出其函数解析式,再把B(2,m)代入反比例函数的解析式即可得出m的值,把AB两点的坐标代入一次函数y=kx+b,求出k、b的值即可得出其解析式;
(2)直接根据函数图象可得出x的取值范围,求出一次函数与x轴的交点坐标,再根据三角形的面积公式即可得出结论.
解答 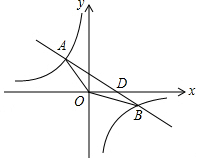 解:(1)∵A(-1,2)在反比例函数y=$\frac{n}{x}$的图象上,
解:(1)∵A(-1,2)在反比例函数y=$\frac{n}{x}$的图象上,
∴n=2×(-1)=-2,
∴其函数解析式为y=-$\frac{2}{x}$;
∵B(2,m)在反比例函数的图象上,
∴m=-$\frac{2}{2}$=-1,
∴B(2,-1).
∵A(-1,2),B(2,-1)两点在一次函数y=kx+b的图象上,
∴$\left\{\begin{array}{l}{-k+b=2}\\{2k+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为:y=-x+1;
(2)∵A(-1,2),B(2,-1),
∴一次函数y=kx+b的值大于反比例函数y=$\frac{n}{x}$的值时,0<x<2或x<-1.
∵一次函数的解析式为:y=-x+1,
∴D(1,0),
∴OD=1,
∴S△OAB=S△OAD+S△OBD=$\frac{1}{2}$×1×2+$\frac{1}{2}$×1×1=1+$\frac{1}{2}$=$\frac{3}{2}$.
点评 本题考查的是反比例函数与一次函数的交点问题,在解答此题时要注意数形结合思想的运用.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.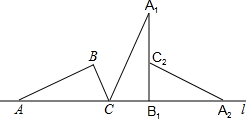 如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB=$\sqrt{3}$,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB=$\sqrt{3}$,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
 如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB=$\sqrt{3}$,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB=$\sqrt{3}$,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )| A. | ($\frac{4}{3}$+$\frac{\sqrt{3}}{2}$)π | B. | ($\frac{25}{12}$+$\frac{\sqrt{3}}{2}$)π | C. | 2π | D. | $\sqrt{3}$π |
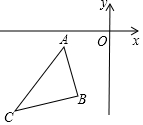 如图,在平面直角坐标系中,点A(-3,-1)、B(-2,-4)、C(-6,-5),以原点位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为(-1,-2)或(1,2).
如图,在平面直角坐标系中,点A(-3,-1)、B(-2,-4)、C(-6,-5),以原点位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为(-1,-2)或(1,2). 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{5}{13}$.
如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{5}{13}$.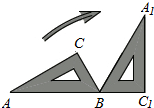 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么旋转角∠CBC1=120°.
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么旋转角∠CBC1=120°.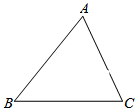 如图,点D在AB上,若点E在AC上,∠B=40°,∠C=70°,当以点A、D、E为顶点的三角形与△ABC相似时,则∠ADE=40°或70°.
如图,点D在AB上,若点E在AC上,∠B=40°,∠C=70°,当以点A、D、E为顶点的三角形与△ABC相似时,则∠ADE=40°或70°.