题目内容
11．
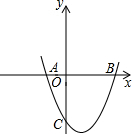如图，已知抛物线y=ax2+bx+c的图象经过A（-1，0）、B（3.0）、C（0．-3）三点．（1）求抛物线的解析式；
（2）把抛物线y=ax2+bx+c配成y=a（x-h）2+k．
分析 （1）由于已知了抛物线与x的两交点坐标，则可设交点式y=a（x+1）（x-3），然后把C点坐标代入计算出a即可．
（2）利用配方法即可得出）y=x2-2x-3=（x-1）2-4．
解答 解：（1）设抛物线的解析式为y=a（x+1）（x-3），
把C（0，-3）代入得a×1×（-3）=-3，
解得a=1，
所以这个二次函数的解析式为y=（x+1）（x-3）=x2-2x-3．
（2）y=x2-2x-3=（x-1）2-4．
点评 本题考查了用待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
1．某初中学校现有学生500人，计划一年后男生增加5%，女生增加4%，这样总人数将增加4.5%，设该校现有男生x人，女生y人，可得方程组为（ ）
| A． | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=4.5%}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=500×4.5%}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=500}\\{105%x+104%y=500+4.5%}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=500}\\{104%x+105%y=500×104.5%}\end{array}\right.$ |
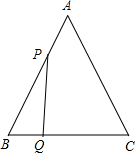已知：如图，△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t（s），解答下列各问题：
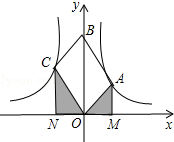如图，OABC是平行四边形，对角线OB在y轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线$y=\frac{k_1}{x}$和y=$\frac{{k}_{2}}{x}$的一支上，分别过点A、C作x轴的垂线，垂足分别为M和N，则有以下的结论：①$\frac{AM}{CN}$=$\frac{|{k}_{1}|}{|{k}_{2}|}$；②阴影部分面积是$\frac{1}{2}$（k1+k2）；③当∠AOC=90°时，|k1|=|k2|；④若OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．其中正确的结论是（ ）
6．
如图是琳琳6个装好糖果的礼包盒，每盒上面的数字代表这盒礼包实际装有的糖果数量．她把其中的5盒送给好朋友小芬和小红，自己留下1盒．已知送的都是整盒，包装没拆过，送给小芬的糖果数量是小红的2倍，则琳琳自己留下的这盒有糖果（ ）
如图是琳琳6个装好糖果的礼包盒，每盒上面的数字代表这盒礼包实际装有的糖果数量．她把其中的5盒送给好朋友小芬和小红，自己留下1盒．已知送的都是整盒，包装没拆过，送给小芬的糖果数量是小红的2倍，则琳琳自己留下的这盒有糖果（ ）| A． | 15粒 | B． | 18粒 | C． | 20粒 | D． | 31粒 |
如图，△ABC中，∠C=90°，AD是角平分线，DE⊥AB于点E，CD=3，BC=8，则BE=（ ）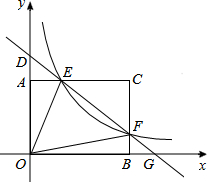
如图，矩形AOBC的顶点坐标分别为A（0，3），O（0，0），B（4，0），C（4，3），动点F在边BC上（不与B、C重合），过点F的反比例函数y=$\frac{k}{x}$的图象与边AC交于点E，直线EF分别与y轴和x轴相交于点D和G，给出下列命题：
20．下列各式计算正确的是（ ）
| A． | 2+$\sqrt{3}$=2$\sqrt{3}$ | B． | 2x-2=$\frac{1}{2{x}^{2}}$ | C． | 3a2•2a3=6a6 | D． | a8÷a2=a6 |
1．
如图，已知AB∥CD，CE交AB于点F，若∠E=20°，∠C=45°，则∠A的度数为（ ）
如图，已知AB∥CD，CE交AB于点F，若∠E=20°，∠C=45°，则∠A的度数为（ ）| A． | 5° | B． | 15° | C． | 25° | D． | 35° |