题目内容
用不同的方法计算:
(1)(3x+2y)2-(3x-2y)2;
(2)(x+y)2+(x-y)2;
(3)(a+2b-c)(a-2b-c)
(1)(3x+2y)2-(3x-2y)2;
(2)(x+y)2+(x-y)2;
(3)(a+2b-c)(a-2b-c)
考点:完全平方公式,平方差公式
专题:计算题
分析:(1)法1:原式利用平方差公式计算即可得到结果;
法2:原式利用完全平方公式展开,去括号合并即可得到结果;
(2)法1:原式利用完全平方公式展开,合并即可得到结果;
法2:原式配方后,计算即可得到结果;
(3)法1:原式利用平方差公式变形,再利用完全平方公式展开即可得到结果;
法2:原式利用多项式乘以多项式法则计算,合并即可得到结果.
法2:原式利用完全平方公式展开,去括号合并即可得到结果;
(2)法1:原式利用完全平方公式展开,合并即可得到结果;
法2:原式配方后,计算即可得到结果;
(3)法1:原式利用平方差公式变形,再利用完全平方公式展开即可得到结果;
法2:原式利用多项式乘以多项式法则计算,合并即可得到结果.
解答:解:(1)法1:原式=[(3x+2y)+(3x-2y)][(3x+2y)-(3x-2y)]
=6x•4y
=24xy;
法2:原式=9x2+12xy+4y2-9x2+12xy-4y2=24xy;
(2)法1:原式=x2+2xy+y2+x2-2xy+y2
=2x2+2y2;
法2:原式=(x+y)2+2(x+y)(x-y)+(x-y)2-2(x+y)(x-y)
=[(x+y)+(x-y)]2-2(x+y)(x-y)
=4x2-2x2+2y2
=2x2+2y2;
(3)法1:原式=(a-c)2-4b2=a2-2ac+c2-4b2;
法2:原式=a2-2ab-ac+2ab-4b2-2bc-ac+2bc+c2=a2-2ac+c2-4b2.
=6x•4y
=24xy;
法2:原式=9x2+12xy+4y2-9x2+12xy-4y2=24xy;
(2)法1:原式=x2+2xy+y2+x2-2xy+y2
=2x2+2y2;
法2:原式=(x+y)2+2(x+y)(x-y)+(x-y)2-2(x+y)(x-y)
=[(x+y)+(x-y)]2-2(x+y)(x-y)
=4x2-2x2+2y2
=2x2+2y2;
(3)法1:原式=(a-c)2-4b2=a2-2ac+c2-4b2;
法2:原式=a2-2ab-ac+2ab-4b2-2bc-ac+2bc+c2=a2-2ac+c2-4b2.
点评:此题考查了完全平方公式,以及平方差公式,熟练掌握公式是解本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
下列说法错误的是( )
| A、-a的绝对值为a | ||
| B、-a的相反数为a | ||
C、
| ||
| D、如果|a|=-a,则a<0或a=0 |
武汉市希望中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
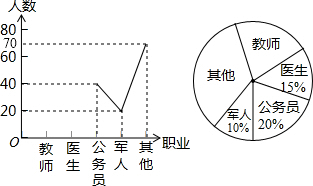

| A、被调查的学生有200人 |
| B、扇形图中公务员部分所对应的圆心角为72° |
| C、被调查的学生中喜欢其他职业的占40% |
| D、被调查的学生中喜欢教师职业的有40人 |
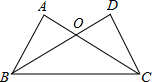 如图,AC与DB相交于点O,已知∠ABC=∠DCB,图中再补充一个条件后可证明△ABC≌△DCB,则这个条件不能是( )
如图,AC与DB相交于点O,已知∠ABC=∠DCB,图中再补充一个条件后可证明△ABC≌△DCB,则这个条件不能是( )| A、AB=DC |
| B、∠A=∠D |
| C、OB=OC |
| D、AC=DB |
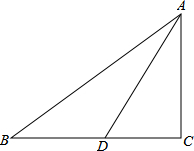 如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=
如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=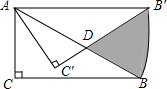 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是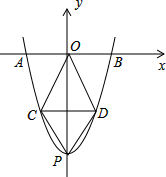 已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,
已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,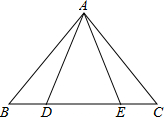 如图D,E是边BC上的两点,AD=AE,∠ADE=∠AED,利用“AAS”方法,请你再添加一个条件:
如图D,E是边BC上的两点,AD=AE,∠ADE=∠AED,利用“AAS”方法,请你再添加一个条件: