题目内容
(1)如图1,在正方形ABCD中,点P在CD上,连接PA,分别过点B、D作BE⊥PA,DF⊥PA,垂足分别为E、F.求证:BE=DF+EF.
(2)在第(1)小题中,当点P在CD的延长线上时,如图2,其他条件不变.试探索BE、DF、EF之间有怎样的数量关系,并对你的结论加以证明.
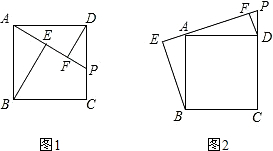
(2)在第(1)小题中,当点P在CD的延长线上时,如图2,其他条件不变.试探索BE、DF、EF之间有怎样的数量关系,并对你的结论加以证明.

考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)如图1,证明∠ABE=∠DAF、∠BAE=∠ADF;进而证明△ABE≌△DAF,即可解决问题.
(2)如图2,类似于(1)中的方法,同理可证△ABE≌△DAF,即可解决问题.
(2)如图2,类似于(1)中的方法,同理可证△ABE≌△DAF,即可解决问题.
解答: 解:(1)如图1,∵四边形ABCD为正方形,
解:(1)如图1,∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°;
∵BE⊥PA,DF⊥PA,
∴∠BAE+∠ABE=∠BAE+∠DAF,
∴∠ABE=∠DAF;同理可证∠BAE=∠ADF;
在△ABE与△DAF中,
,
∴△ABE≌△DAF(ASA),
∴BE=AF,AE=DF,
∴BE=DF+EF.
(2)EF=BE+DF.理由如下:
如图2,类似于(1)中的方法,
同理可证△ABE≌△DAF,
∴BE=AF,AE=DF,
∴EF=BE+DF.
 解:(1)如图1,∵四边形ABCD为正方形,
解:(1)如图1,∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°;
∵BE⊥PA,DF⊥PA,
∴∠BAE+∠ABE=∠BAE+∠DAF,
∴∠ABE=∠DAF;同理可证∠BAE=∠ADF;
在△ABE与△DAF中,
|
∴△ABE≌△DAF(ASA),
∴BE=AF,AE=DF,
∴BE=DF+EF.
(2)EF=BE+DF.理由如下:
如图2,类似于(1)中的方法,
同理可证△ABE≌△DAF,
∴BE=AF,AE=DF,
∴EF=BE+DF.
点评:该题以正方形为载体,主要考查了正方形的性质、全等三角形的判定及其性质的应用等几何知识点;牢固掌握正方形的性质、全等三角形的判定及其性质是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
多项式7x2+x-1与多项式M的差是3x2-6x+5,则多项式M是( )
| A、4x2-5x+4 |
| B、10x2-5x+4 |
| C、4x2+7x-6 |
| D、-4x2-7x+6 |
 如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )
如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )| A、2cm | B、4cm |
| C、6cm | D、3cm |
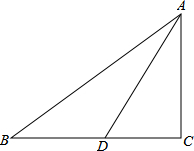 如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=
如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=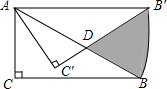 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是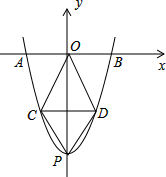 已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,
已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,