题目内容
17．
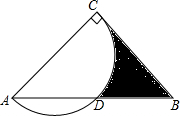如图，在等腰Rt△ABC中，∠ACB=90°，AC=4，以边AC为直径的半圆交AB于点D，则图中阴影部分的面积是6-π（结果保留π）
分析 连接OD、CD，根据等腰三角形的性质得到AD=DB，根据三角形中位线定理求出OD，根据梯形的面积公式、扇形面积公式计算即可．
解答 解：
连接OD、CD，
∵AC为半圆的直径，
∴CD⊥AB，
∵CA=CB，
∴AD=DB，又AO=OC，
∴OD=$\frac{1}{2}$BC=2，∠COD=∠ACB=90°，
∴图中阴影部分的面积是=$\frac{1}{2}$×（2+4）×2-$\frac{90π×{2}^{2}}{360}$=6-π，
故答案为：6-π．
点评 本题考查的是扇形面积的计算，掌握扇形的面积公式、三角形中位线定理、梯形的面积公式是解题的关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，△A1B1C1由△ABC绕某点旋转而成，请你用尺规作图，找出旋转中心O，并用量角器度量出旋转的大小（完成填空）．旋转角（∠COC1）是90度．
如图所示，小月家有四边形的田地ACBD，测量得∠ACB=∠ABD=90°，CA=CB，∠DAB=30°，AD=80cm，求这块菜地的面积是多少？
如图，已知△ABC中，BE=3AE，CD=2AD，若△ADE的面积为1平方厘米，求三角形ABC的面积．
已知a、b、c位置如图所示，试化简：|a+b-c|+$\sqrt{（b-a）^{2}}$=-2a+c．