题目内容
2．代数式x2+6x-8，当x=-3时有最小值是-17．分析 利用配方法将代数式x2+6x-8变形为（x+3）2-17，再根据偶次方的非负性即可解决最值问题，
解答 解：∵x2+6x-8=x2+6x+9-17=（x+3）2-17≥-17，
∴当x=-3时，代数式x2+6x-8有最小值-17．
故答案为：-3；小；-17．
点评 本题考查了配方法的应用以及偶次方的非负性，利用配方法将代数式x2+6x-8变形为（x+3）2-17是解题的关键．
练习册系列答案
相关题目
10．
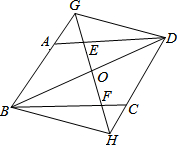如图，在平行四边形ABCD中，AB=3，BC=4，∠ABC=60°，过对角线BD的中点O的直线GH分别交AD、BC于点E、F，交BA的延长线于点G，交DC的延长线于点H，连结GD、BH，则下列结论：①AG=CH，②DE+CF=5，③S四边形ABFE=3$\sqrt{3}$，④四边形BGDH为平行四边形．其中正确的有（ ）
如图，在平行四边形ABCD中，AB=3，BC=4，∠ABC=60°，过对角线BD的中点O的直线GH分别交AD、BC于点E、F，交BA的延长线于点G，交DC的延长线于点H，连结GD、BH，则下列结论：①AG=CH，②DE+CF=5，③S四边形ABFE=3$\sqrt{3}$，④四边形BGDH为平行四边形．其中正确的有（ ）| A． | ②③④ | B． | ①③④ | C． | ①②④ | D． | ①②③ |
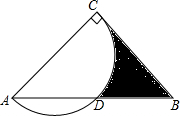如图，在等腰Rt△ABC中，∠ACB=90°，AC=4，以边AC为直径的半圆交AB于点D，则图中阴影部分的面积是6-π（结果保留π）