题目内容
1. 如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CE相交于点D,则①△ABE≌△ACF,②△BDF≌CDE,③点D在∠BAC的平分线上,以上结论正确的是( )
如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CE相交于点D,则①△ABE≌△ACF,②△BDF≌CDE,③点D在∠BAC的平分线上,以上结论正确的是( )| A. | ① | B. | ② | C. | ①② | D. | ①②③ |
分析 连接AD.由△ABE≌△ACF,故①正确,推出AE=AF,由AB=AC,推出EC=BF,推出△DEC≌△DFB,故②正确,推出DE=DF,由DE⊥AC,DF⊥AB,推出DA平分∠CAB,故③正确.
解答 解:如图,连接AD.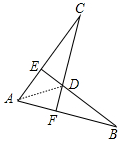
∵BE⊥AC于点E,CF⊥AB于点F,
∴∠AEB=∠AFC=90°,∠DEC=∠DFB=90°,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{∠AEB=∠AFC}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACF,故①正确,
∴AE=AF,∵AB=AC,
∴EC=BF,
在△DEC和△DFB中,
$\left\{\begin{array}{l}{∠EDC=∠FDB}\\{∠DEC=∠DFB}\\{EC=FB}\end{array}\right.$,
∴△DEC≌△DFB,故②正确,
∴DE=DF,∵DE⊥AC,DF⊥AB,
∴DA平分∠CAB,故③正确,
故选D.
点评 本题考查全等三角形的判定和性质、角平分线的判定定理等知识,解题的关键是灵活运用全等三角形的判定和性质解决问题,属于中考常考题型.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.

(1)根据图中提供的信息填表:
则S=$\frac{1}{2}$m+n-1(用含m、n的代数式表示)
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=m+2(n-1)(用含m、n的代数式表示).


(1)根据图中提供的信息填表:
| 格点多边形各边上的 格点的个数 | 格点边多边形内部的 格点个数 | 格点多边形的面积 | |
| 多边形1 | 4 | 1 | 2 |
| 多边形2 | 5 | 2 | ②$\frac{7}{2}$ |
| 多边形3 | 6 | 3 | 5 |
| 多边形4 | ①5 | 4 | $\frac{11}{2}$ |
| 一般格点多边形 | m | n | S |
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=m+2(n-1)(用含m、n的代数式表示).

13.非等边三角形的三条边都是方程x2-6x+8=0的解,则这个三角形的周长是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 8 或 10 |
10.如图,水平地面上有一面积为30πcm2的灰色扇形OAB,其中OA=6cm,且OA垂直于地面,将这个扇形向右滚动(无滑动)至点B刚好接触地面为止,则在这个滚动过程中,点O移动的距离是( )
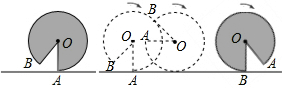

| A. | 10πcm | B. | 20πcm | C. | 24πcm | D. | 30πcm |
 已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.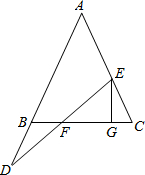 如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
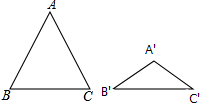 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为25:9.
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为25:9.