题目内容
11.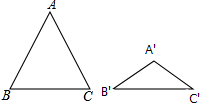 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为25:9.
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为25:9.
分析 先根据等腰三角形的性质得到∠B=∠C,∠B′=∠C′,根据三角函数的定义得到AD=AB•sinB,A′D′=A′B′•sinB′,BC=2BD=2AB•cosB,B′C′=2B′D′=2A′B′•cosB′,然后根据三角形面积公式即可得到结论.
解答 解:过A作AD⊥BC于D,过A′作A′D′⊥B′C′于D′,
∵△ABC与△A′B′C′都是等腰三角形,
∴∠B=∠C,∠B′=∠C′,BC=2BD,B′C′=2B′D′,
∴AD=AB•sinB,A′D′=A′B′•sinB′,BC=2BD=2AB•cosB,B′C′=2B′D′=2A′B′•cosB′,
∵∠B+∠B′=90°,
∴sinB=cosB′,sinB′=cosB,
∵S△BAC=$\frac{1}{2}$AD•BC=$\frac{1}{2}$AB•sinB•2AB•cosB=25sinB•cosB,
S△A′B′C′=$\frac{1}{2}$A′D′•B′C′=$\frac{1}{2}$A′B′•cosB′•2A′B′•sinB′=9sinB′•cosB′,
∴S△BAC:S△A′B′C′=25:9,
故答案为:25:9.
点评 本题考查了互余两角的关系,解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰三角形的性质和三角形面积公式.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1. 如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CE相交于点D,则①△ABE≌△ACF,②△BDF≌CDE,③点D在∠BAC的平分线上,以上结论正确的是( )
如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CE相交于点D,则①△ABE≌△ACF,②△BDF≌CDE,③点D在∠BAC的平分线上,以上结论正确的是( )
 如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CE相交于点D,则①△ABE≌△ACF,②△BDF≌CDE,③点D在∠BAC的平分线上,以上结论正确的是( )
如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CE相交于点D,则①△ABE≌△ACF,②△BDF≌CDE,③点D在∠BAC的平分线上,以上结论正确的是( )| A. | ① | B. | ② | C. | ①② | D. | ①②③ |
2.直线外一点距离此直线3cm,以该点为顶点作等腰直角三角形,使另两顶点在该直线上,这样的等腰直角三角形的面积是( )
| A. | 3cm2,4.5cm2,9cm2 | B. | 4.5cm2,9cm2 | ||
| C. | 3cm2,9cm2 | D. | 3cm2,4.5cm2 |
6.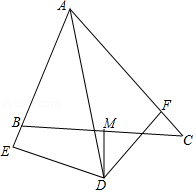 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
①DE=DF;②DE+DF=AD;③DM平分∠EDF;④AB+AC=2AE;
其中正确的有( )
 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠EDF;④AB+AC=2AE;
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.已知$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$且-1<x-y<0,则k的取值范围为( )
| A. | -1<k<-$\frac{1}{2}$ | B. | $\frac{1}{2}$<k<1 | C. | 0<k<1 | D. | 0<k<$\frac{1}{2}$ |
1.下列式子中,从左到右的变形是因式分解的是( )
| A. | (x-1)(x-2)=x2-3x+2 | B. | x2+4x+4=x(x+4)+4 | C. | x2-4=(x+2)(x-2) | D. | x2+y2=(x+y)(x-y) |