题目内容
18.把一根长30cm的铁丝分为两部分,每一部分均弯曲成一个正三角形,它们的面积和的最小值是$\frac{25\sqrt{3}}{2}$cm2.分析 设第一个等边三角形的边长为xcm,则第二个等边三角形的边长为(10-x)cm,设两个三角形的面积和为y,根据等边三角形的性质结合三角形的面积公式即可得出y关于x的二次函数关系式,利用配方法结合二次函数的性质即可解决最值问题.
解答 解:设第一个等边三角形的边长为xcm,则第二个等边三角形的边长为(10-x)cm,设两个三角形的面积和为y,
根据题意得:y=$\frac{\sqrt{3}}{4}$x2+$\frac{\sqrt{3}}{4}$(10-x)2=$\frac{\sqrt{3}}{2}$x2-5$\sqrt{3}$x+25$\sqrt{3}$=$\frac{\sqrt{3}}{2}$(x-5)2+$\frac{25\sqrt{3}}{2}$.
∵$\frac{\sqrt{3}}{2}$>0,
∴当x=5时,y取最小值,最小值为$\frac{25\sqrt{3}}{2}$.
故答案为:$\frac{25\sqrt{3}}{2}$.
点评 本题考查了二次函数的应用以及等边三角形的性质,解题的关键是得出y关于x的二次函数关系式.本题属于基础题,难度不大,解决该题型题目时,根据三角形的面积找出y关于x的函数关系式是关键.

练习册系列答案
相关题目
9.我们知道,在弹性限度内,弹簧挂上重物后会伸长.已知一根弹簧的长度(cm)与所挂重物的质量(kg)之间的关系如下表,则下列说法错误的是( )
| 重物的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
| A. | 在这一变化过程中,重物的质量是自变量,弹簧的长度是因变量 | |
| B. | 当所挂重物的质量是4kg时,弹簧的长度是14cm | |
| C. | 在弹性限度内,当所挂重物的质量是6kg时,弹簧的长度是16cm | |
| D. | 当不挂重物时,弹簧的长度应为12cm |
10.从8:10到8:32分,时钟的分针转过的角度为( )
| A. | 122° | B. | 132° | C. | 135° | D. | 150° |
 有理数在数轴上的对应的点如图,化简代数式:
有理数在数轴上的对应的点如图,化简代数式: 如图,已知∠1=20°,∠2=30°,∠A=50°,求∠BDC的度数.
如图,已知∠1=20°,∠2=30°,∠A=50°,求∠BDC的度数.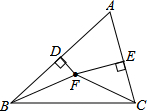 如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.
如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.