题目内容
13.已知A=3x2-5x-2,B=4x+7,当x为何值时A=B?分析 根据题意先把方程进行整理,再找出一元二次方程中的二次项系数a,一次项系数b及常数项c,计算出根的判别式大于0,然后将a,b及c的值代入求根公式,即可求出方程的解.
解答 解:∵A=3x2-5x-2,B=4x+7,
∴3x2-5x-2=4x+7时,A=B,
∴x2-3x-3=0,
∵a=1,b=-3,c=-3,
∴△=b2-4ac=9+12=21>0,
∴x=$\frac{3±\sqrt{21}}{2}$,
∴x1=$\frac{3+\sqrt{21}}{2}$,x2=$\frac{3-\sqrt{21}}{2}$.
点评 此题考查了公式法解一元二次方程,利用此方法解方程时,首先将方程化为一般形式,找出a,b及c的值,然后计算出根的判别式b2-4ac的值,当b2-4ac≥0,将a,b,c的值代入求根公式即可求出解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.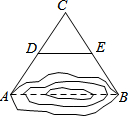 如图,A,B两点位于一个池塘的两端,冬冬想用绳子测量A,B两点间的距离,但绳子不够长,一位同学帮他想了一个办法:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测得DE的长为15m,则A,B两点间的距离为( )
如图,A,B两点位于一个池塘的两端,冬冬想用绳子测量A,B两点间的距离,但绳子不够长,一位同学帮他想了一个办法:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测得DE的长为15m,则A,B两点间的距离为( )
 如图,A,B两点位于一个池塘的两端,冬冬想用绳子测量A,B两点间的距离,但绳子不够长,一位同学帮他想了一个办法:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测得DE的长为15m,则A,B两点间的距离为( )
如图,A,B两点位于一个池塘的两端,冬冬想用绳子测量A,B两点间的距离,但绳子不够长,一位同学帮他想了一个办法:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测得DE的长为15m,则A,B两点间的距离为( )| A. | 7.5m | B. | 15m | C. | 22.5m | D. | 30m |
5.一件商品降价10%之后,再涨价10%卖了99元,原价是( )
| A. | 121元 | B. | 81元 | C. | 98.01元 | D. | 100元 |
 如图所示,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m,若灯泡距离地面2m,则地面上阴影部分的面积为1.44πm2.
如图所示,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m,若灯泡距离地面2m,则地面上阴影部分的面积为1.44πm2. 如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于F.
如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于F. 如图,有一个水池,其中CD为$\frac{5}{3}$m,池中央垂直长了一根芦苇,露出水面的部分高$\frac{1}{3}$m,把芦苇的顶端引到岸边,苇顶和岸边水面刚好齐平,求水深和芦苇的高度.
如图,有一个水池,其中CD为$\frac{5}{3}$m,池中央垂直长了一根芦苇,露出水面的部分高$\frac{1}{3}$m,把芦苇的顶端引到岸边,苇顶和岸边水面刚好齐平,求水深和芦苇的高度. 知者加速:
知者加速: