题目内容
6.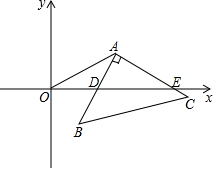 如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.
如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.(1)求A点坐标;
(2)若平面内有一点M,使四边形ADOM组成菱形,求D点坐标;
(3)当△ABC绕直角顶点A旋转过程中,若另一直角边AC与x轴交于E,此时$\frac{1}{A{D}^{2}}$+$\frac{1}{A{E}^{2}}$的值是否发生变化?若不变,求$\frac{1}{A{D}^{2}}$+$\frac{1}{A{E}^{2}}$的值是多少?若改变请说明理由.
分析 (1)根据非负数的性质列出算式,求出a、b的值,得到A点坐标;
(2)作AN⊥x轴于点N,设OD=x,根据菱形的四条边相等列出方程,解方程即可;
(3)根据三角形的面积公式得到AD×AE=DE×AN,根据勾股定理、分式的加减运算法则计算即可.
解答 解:(1)由题意得,a-8=0,b-4=0,
解得,a=8,b=4,
则点A的坐标为(8,4);
(2)作AN⊥x轴于点N,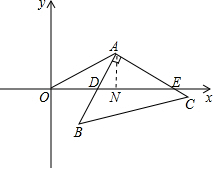
∵四边形ADOM组成菱形,
∴OD=AD,
设OD=x,则AD=x,DN=8-x
在Rt△ADN中AD2=DN2+AN2
即x2=(8-x)2+42,
解得,x=5
∴D坐标(5,0);
(3)$\frac{1}{A{D}^{2}}$+$\frac{1}{A{E}^{2}}$的值不变,
∵S△ADE=$\frac{1}{2}$×AD×AE=$\frac{1}{2}$×DE×AN,
∴AD×AE=DE×AN,
∴AD2×AE2=DE2×AN2,
则$\frac{1}{A{D}^{2}}$+$\frac{1}{A{E}^{2}}$=$\frac{A{D}^{2}+A{E}^{2}}{A{D}^{2}×A{E}^{2}}$=$\frac{D{E}^{2}}{D{E}^{2}×A{N}^{2}}$
=$\frac{1}{A{N}^{2}}$
=$\frac{1}{16}$.
点评 本题考查的是菱形的性质、非负数的性质,掌握菱形的四条边相等、灵活运用三角形的面积公式是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.
如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.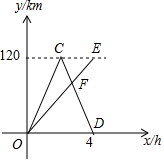 A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.
A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象. 如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.
如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.