题目内容
17.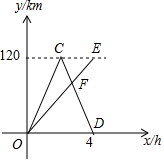 A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.
A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.(1)求甲车返回时(即CD段)y与x之间的函数解析式;
(2)若当它们行驶了2.5h时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当两车相距30km时,甲车行驶的时间为$\frac{5}{4}$h、$\frac{35}{16}$h、$\frac{45}{16}$h.
分析 (1)根据题意和函数图象中的数据可以求得甲车返回时(即CD段)y与x之间的函数解析式;
(2)根据题意和函数图象中的数据可以求得当它们行驶了2.5h时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)根据题意可以列出相应的方程,求出当两车相距30km时,甲车行驶的时间.
解答 解:(1)由题意可得,
点C的坐标为(2,120),点D的坐标为(4,0),
设甲车返回时(即CD段)y与x之间的函数解析式为y=kx+b,
$\left\{\begin{array}{l}{120=2k+b}\\{0=4k+b}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-60}\\{b=240}\end{array}\right.$,
即甲车返回时(即CD段)y与x之间的函数解析式为y=-60x+240;
(2)将x=2.5代入y=-60x+240,得
y=-60×2.5+240=90,
∴点F的坐标为(2.5,90),
∴乙车的速度为:90÷2.5=36km/h,乙车从A地到B地用的时间为:120÷36=$\frac{10}{3}$h,
设乙车行驶过程中y与x之间的函数解析式为y=ax,
90=a×2.5,得a=36,
即乙车的速度是35km/h,乙车行驶过程中y与x之间的函数解析式是y=36x(0≤x≤$\frac{10}{3}$);
(3)设OC段对应的函数解析式为y=mx,
120=m×2,得m=60,
即OC段对应的函数解析式为y=60x,
∴60x-36x=30,得x=$\frac{5}{4}$,
|(-60x+240)-36x|=30,得${x}_{1}=\frac{35}{16}$,${x}_{2}=\frac{45}{16}$,
故答案为:$\frac{5}{4}$h、$\frac{35}{16}$h、$\frac{45}{16}$.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用数形结合的思想解答.

 口算题天天练系列答案
口算题天天练系列答案| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
①内错角相等;②过直线外一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④幂的乘方,底数不变,指数相加;⑤两个角的和为90°,则这两个角互补.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 1 | B. | 3 | C. | -1 | D. | -3 |
 已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.
已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.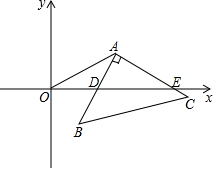 如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.
如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.