题目内容
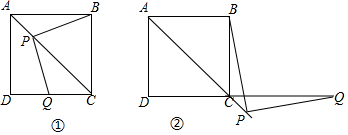
11. 如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.
如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.
分析 根据平行线的性质,即可得到∠3的度数,再根据平角的定义以及折叠的性质,即可得到∠2的度数.
解答  解:根据长方形的对边平行,可得
解:根据长方形的对边平行,可得
∠1+∠3=180°,
∵∠1=100°,
∴∠3=80°,
由折叠可得,∠2=∠4=$\frac{1}{2}$(180°-80°)=50°,
故答案为:50
点评 本题主要考查了平行线的性质以及折叠的性质,解题时注意:两直线平行,同旁内角互补.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2.下列说法正确的是( )
①内错角相等;②过直线外一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④幂的乘方,底数不变,指数相加;⑤两个角的和为90°,则这两个角互补.
①内错角相等;②过直线外一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④幂的乘方,底数不变,指数相加;⑤两个角的和为90°,则这两个角互补.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.已知2-$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根,则方程的另一个根与c的值是( )
| A. | $\sqrt{3}$-2,-1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | 2+$\sqrt{3}$,1 | D. | 2+$\sqrt{3}$,7-4$\sqrt{3}$ |
20.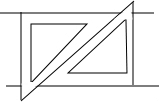 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 平行于同一条直线的两直线平行 |
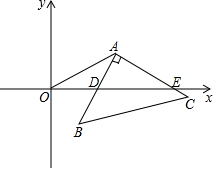 如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.
如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.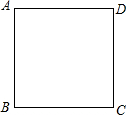 在正方形ABCD中,点E是边BC上的中点,在边CD上取一点F,使得AE平分∠BAF.
在正方形ABCD中,点E是边BC上的中点,在边CD上取一点F,使得AE平分∠BAF.