题目内容
1．在△ABC中，∠C=90°，若AB=2，则AB2+AC2+BC2=8．分析 根据勾股定理得到AC2+BC2=AB2=4，计算即可．
解答 解：∵∠C=90°，
由勾股定理得，AC2+BC2=AB2=4，
∴AB2+AC2+BC2=4+4=8，
故答案为：8．
点评 本题考查的是勾股定的应用，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
相关题目
9．已知两个变量之间的关系满足y=-x+2，则当x=-1时，对应的y的值为（ ）
| A． | 1 | B． | 3 | C． | -1 | D． | -3 |
16．
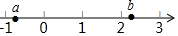已知a，b在数轴上的位置如图所示，化简代数式$\sqrt{（a-1）^{2}}$-$\sqrt{（a+b）^{2}}$+|1-b|的结果等于（ ）
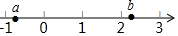已知a，b在数轴上的位置如图所示，化简代数式$\sqrt{（a-1）^{2}}$-$\sqrt{（a+b）^{2}}$+|1-b|的结果等于（ ）| A． | -2a | B． | -2b | C． | -2a-b | D． | 2 |
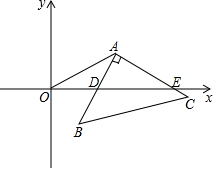如图，平面直角坐标系中有一点A（a，b），且满足$\sqrt{a-8}$+（b-4）2=0，将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转，直角边AB与x轴始终交于D，连接OA．
