题目内容
1．
如图，AB∥CD，CB平分∠ACD．若∠BCD=28°，则∠A的度数为124°．
分析 根据平行线的性质得到∠ABC=∠BCD=28°，根据角平分线的定义得到∠ACB=∠BCD=28°，根据三角形的内角和即可得到结论．
解答 解：∵AB∥CD，
∴∠ABC=∠BCD=28°，
∵CB平分∠ACD，
∴∠ACB=∠BCD=28°，
∴∠A=180°-∠ABC-∠ACB=124°，
故答案为：124°．
点评 本题考查了平行线的性质，角平分线的定义，三角形的内角和，熟练掌握平行线的性质是解题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
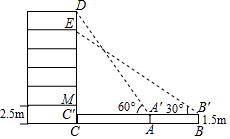如图，某数学兴趣小组要测量一栋五层居民楼CD的高度．该楼底层为车库，高2.5米；上面五层居住，每层高度相等．测角仪支架离地1.5米，在A处测得五楼顶部点D的仰角为60°，在B处测得四楼顶部点E的仰角为30°，AB=14米．求居民楼的高度（精确到0.1米，参考数据：$\sqrt{3}$≈1.73）
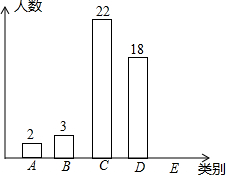某班为了解学生一学期做义工的时间情况，对全班50名学生进行调查，按做义工的时间t（单位：小时），将学生分成五类：A类（0≤t≤2），B类（2＜t≤4），C类（4＜t≤6），D类（6＜t≤8），E类（t＞8）．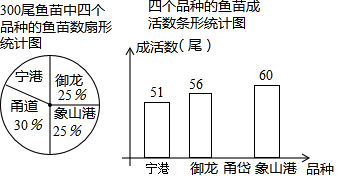
如图，四边形ABCD为平行四边形，F是CD的中点，连接AF并延长与BC的延长线交于点E．求证：BC=CE．
13．一个三角形的三个内角的度数之比为1：2：3，则这个三角形一定是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 等腰直角三角形 |
10．下列式子为最简二次根式的是（ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{12}$ | C． | $\sqrt{a^2}$ | D． | $\sqrt{\frac{1}{a}}$ |
如图，已知⊙O是△ABC的外接圆，连接AO，若∠B=40°，则∠OAC=50°．