题目内容
9. 某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).
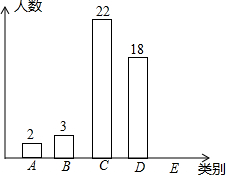
某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
(1)E类学生有5人,补全条形统计图;
(2)D类学生人数占被调查总人数的36%;
(3)从该班做义工时间在0≤t≤4的学生中任选2人,求这2人做义工时间都在2<t≤4中的概率.
分析 (1)根据总人数等于各类别人数之和可得E类别学生数;
(2)用D类别学生数除以总人数即可得;
(3)列举所有等可能结果,根据概率公式求解可得.
解答 解:(1)E类学生有50-(2+3+22+18)=5(人),
补全图形如下:
故答案为:5;
(2)D类学生人数占被调查总人数的$\frac{18}{50}$×100%=36%,
故答案为:36;
(3)记0≤t≤2内的两人为甲、乙,2<t≤4内的3人记为A、B、C,
从中任选两人有:甲乙、甲A、甲B、甲C、乙A、乙B、乙C、AB、AC、BC这10种可能结果,
其中2人做义工时间都在2<t≤4中的有AB、AC、BC这3种结果,
∴这2人做义工时间都在2<t≤4中的概率为$\frac{3}{10}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查条形统计图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏.游戏规则:转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.甲获胜的概率是( )


| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
4. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )| A. | AD=2OB | B. | CE=EO | C. | ∠OCE=40° | D. | ∠BOC=2∠BAD |
18.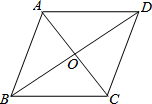 如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
 如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )| A. | 5cm | B. | 10cm | C. | 14cm | D. | 20cm |
 国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.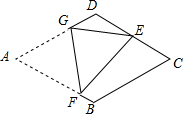 如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则cos∠EFG的值为$\frac{\sqrt{21}}{7}$.
如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则cos∠EFG的值为$\frac{\sqrt{21}}{7}$. 如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.
如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.