题目内容
12.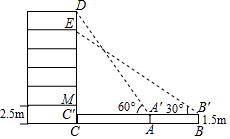 如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:$\sqrt{3}$≈1.73)
如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:$\sqrt{3}$≈1.73)
分析 设每层楼高为x米,由MC-CC′求出MC′的长,进而表示出DC′与EC′的长,在直角三角形DC′A′中,利用锐角三角函数定义表示出C′A′,同理表示出C′B′,由C′B′-C′A′求出AB 的长即可.
解答 解:设每层楼高为x米,
由题意得:MC′=MC-CC′=2.5-1.5=1米,
∴DC′=5x+1,EC′=4x+1,
在Rt△DC′A′中,∠DA′C′=60°,
∴C′A′=$\frac{DC′}{tan60°}$=$\frac{\sqrt{3}}{3}$(5x+1),
在Rt△EC′B′中,∠EB′C′=30°,
∴C′B′=$\frac{EC′}{tan30°}$=$\sqrt{3}$(4x+1),
∵A′B′=C′B′-C′A′=AB,
∴$\sqrt{3}$(4x+1)-$\frac{\sqrt{3}}{3}$(5x+1)=14,
解得:x≈3.17,
则居民楼高为5×3.17+2.5≈18.4米.
点评 此题属于解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
2.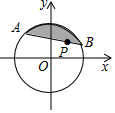 如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为($\sqrt{2}$,$\sqrt{2}$),弦AB经过点P,则图中阴影部分面积的最小值等于( )
如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为($\sqrt{2}$,$\sqrt{2}$),弦AB经过点P,则图中阴影部分面积的最小值等于( )
 如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为($\sqrt{2}$,$\sqrt{2}$),弦AB经过点P,则图中阴影部分面积的最小值等于( )
如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为($\sqrt{2}$,$\sqrt{2}$),弦AB经过点P,则图中阴影部分面积的最小值等于( )| A. | 2π-4 | B. | 4π-8 | C. | $\frac{8π-6\sqrt{3}}{3}$ | D. | $\frac{16π-12\sqrt{3}}{3}$ |
20.甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏.游戏规则:转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.甲获胜的概率是( )


| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
7.若代数式$\frac{\sqrt{x-2}}{\sqrt{x-1}}$有意义,则实数x的取值范围是( )
| A. | x≥1 | B. | x≥2 | C. | x>1 | D. | x>2 |
4. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )| A. | AD=2OB | B. | CE=EO | C. | ∠OCE=40° | D. | ∠BOC=2∠BAD |
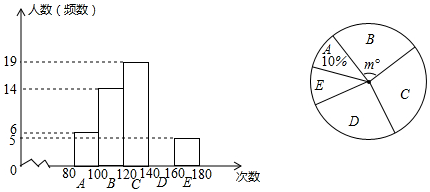
 国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h. 如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.
如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.