题目内容
11.在矩形ABCD中,AB=3,BC=6,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C、D的对应点分别为C′、D′,折痕与边AD交于点F,当点B、C′、D′恰好在同一直线上时,AF的长为4$+\sqrt{3}$或4-$\sqrt{3}$.分析 由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE,在Rt△BC′E中,由于$\frac{BE}{C′E}$=2,得到∠C′BE=30°,①当点C′在BC的上方时,如图1,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形根据等边三角形的性质和矩形的性质即可得到AF═4+$\sqrt{3}$,②当点C′在BC的下方时,如图2,过F作FG⊥AD于G,D′F交BE于H,同①可得四边形ABGF是矩形根据矩形的性质和等边三角形的性质即可得到AF=4-$\sqrt{3}$.
解答  解:由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE,
解:由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE,
∵点B、C′、D′在同一直线上,
∴∠BC′E=90°,
∵BC=6,BE=2CE,
∴BE=4,C′E=CE=2,
在Rt△BC′E中,$\frac{BE}{C′E}$=2,
∴∠C′BE=30°,
①当点C′在BC的上方时,
如图1,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形,
∴EG=AB=3,AG=BE=4,
∵∠C′BE=30°,∠BC′E=90°,
∴∠BEC′=60°,
由折叠的性质得,∠C′EF=′CEF,
∴∠C′EF=∠CEF=60°,
∵AD∥BC,
∴∠HFE=∠CEF=60°,
∴△EFH是等边三角形,
∴在Rt△EFG中,EG=3,
∴GF=$\sqrt{3}$,
∴AF═4+$\sqrt{3}$,
②当点C′在BC的下方时,如图2,过F作FG⊥AD于G,D′F交BE于H,同①可得四边形ABGF是矩形,△EFH是等边三角形,
∴AF=BG,FG=AB=3,∠FEH=60°,
在Rt△EFG中,GE=$\sqrt{3}$,
∵BE=4,
∴BG=4-$\sqrt{3}$,
∴AF=4-$\sqrt{3}$,
综上所述,AF的长是4$+\sqrt{3}$或4-$\sqrt{3}$.
故答案为:4$+\sqrt{3}$或4-$\sqrt{3}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,等边三角形的判定和性质,正确的作出图形是解题的关键.

 金钥匙试卷系列答案
金钥匙试卷系列答案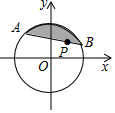 如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为($\sqrt{2}$,$\sqrt{2}$),弦AB经过点P,则图中阴影部分面积的最小值等于( )
如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为($\sqrt{2}$,$\sqrt{2}$),弦AB经过点P,则图中阴影部分面积的最小值等于( )| A. | 2π-4 | B. | 4π-8 | C. | $\frac{8π-6\sqrt{3}}{3}$ | D. | $\frac{16π-12\sqrt{3}}{3}$ |

| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
 如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.
如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.