题目内容
6. 如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.求证:BC=CE.
如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.求证:BC=CE.
分析 根据平行四边形的对边平行且相等可得AD=BC,AD∥BC,根据两直线平行,内错角相等可得∠DAF=∠E,∠ADF=∠ECF,根据线段中点的定义可得DF=CF,然后利用“角角边”证明△ADF≌△ECF,根据全等三角形对应边相等可得AD=CE,从而得证.
解答  证明:如图,∵四边形ABCD是平行四边形,
证明:如图,∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
又∵F是CD的中点,即DF=CF,
∴△ADF≌△ECF,
∴AD=CE,
∴BC=CE.
点评 本题考查了平行四边形的性质,全等三角形的判定与性质,熟记性质并确定出三角形全等的条件是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列计算正确的是( )
| A. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | B. | a+2a=2a2 | C. | x(1+y)=x+xy | D. | (mn2)3=mn6 |
18.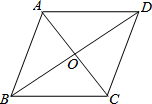 如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
 如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )| A. | 5cm | B. | 10cm | C. | 14cm | D. | 20cm |
16.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.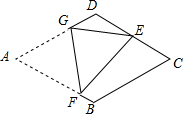 如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则cos∠EFG的值为$\frac{\sqrt{21}}{7}$.
如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则cos∠EFG的值为$\frac{\sqrt{21}}{7}$. 如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.
如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为124°.