题目内容
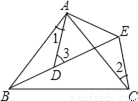
如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.
 55°
【解析】求出∠BAD=∠EAC,证△BAD≌△EAC,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解析】
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△EAC中,
AB=AC,∠BAD=∠EAC,
∴△BAD≌△EAC(SAS),
∴∠2=∠ABD=30°,
∵...
55°
【解析】求出∠BAD=∠EAC,证△BAD≌△EAC,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解析】
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△EAC中,
AB=AC,∠BAD=∠EAC,
∴△BAD≌△EAC(SAS),
∴∠2=∠ABD=30°,
∵...
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
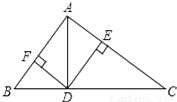
期末集结号系列答案如图,在直角三角形ABC中,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(除之C外)相等的角的个数是( )
A. 2 B. 3 C. 4 D. 5
 B
【解析】试题分析:图中与∠C(除之C外)相等的角有∠ADE、∠FAD、∠FDB共3个,故答案选B.
B
【解析】试题分析:图中与∠C(除之C外)相等的角有∠ADE、∠FAD、∠FDB共3个,故答案选B. 自由转动如图所示的转盘.下列事件中哪些是必然事件?那些是随机事件?根据你的经验,将这些事件的序号按发生的可能性从小到大的顺序排列.
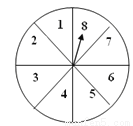
(1)转盘停止后指针指向1;
(2)转盘停止后指针指向10;
(3)转盘停止后指针指向的是偶数;
(4)转盘停止后指针指向的不是奇数就是偶数;
(5)转盘停止后指针指向的数大于1.
 (2)(1)(3)(5)(4).
【解析】
试题分析:根据可能性等于所求情况数与总情况数之比分别求出每种情况的可能性,再按发生的可能性从小到大的顺序排列即可.
试题解析:(1)转盘停止后指针指向1的概率是;
(2)转盘停止后指针指向10的概率是0;
(3)转盘停止后指针指向的是偶数的概率是;
(4)转盘停止后指针指向的不是奇数就是偶数的概率是=1;
(5)...
(2)(1)(3)(5)(4).
【解析】
试题分析:根据可能性等于所求情况数与总情况数之比分别求出每种情况的可能性,再按发生的可能性从小到大的顺序排列即可.
试题解析:(1)转盘停止后指针指向1的概率是;
(2)转盘停止后指针指向10的概率是0;
(3)转盘停止后指针指向的是偶数的概率是;
(4)转盘停止后指针指向的不是奇数就是偶数的概率是=1;
(5)... 2014年3月,YC市举办了首届中学生汉字听写大会,从甲、乙、丙、丁4套题中随机抽取一套训练,抽中甲的概率是( )
A.  B.
B. 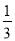 C.
C. 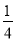 D.
D. 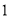
 C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C.
C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C. 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是___________.
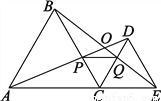
 ①②③⑤
【解析】试题解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=
∴△PC...
①②③⑤
【解析】试题解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=
∴△PC... 如图,线段AD把△ABC分为面积相等的两部分,则线段AD是( ).
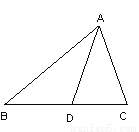
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
 B
【解析】试题分析:三角形的中线将三角形的面积分成相等的两部分,角平分线是指将角分成度数相等的两个角.
B
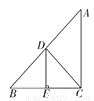
【解析】试题分析:三角形的中线将三角形的面积分成相等的两部分,角平分线是指将角分成度数相等的两个角. 如图所示,AB-AC=2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,
求AB和AC的长.
 AB=8,AC=6
【解析】试题分析:根据线段垂直平分线性质求出BD=DC,根据三角形周长求出AB+AC=12cm,根据已知得出AC=AB-2cm,即可求出答案.
试题解析:
∵DE垂直平分BC,
∴BD=CD.
∴△ACD的周长=AD+AC+CD=AD+AC+BD=AB+AC=14cm.
解方程组
得
∴AC=6cm,AB=8cm.
AB=8,AC=6
【解析】试题分析:根据线段垂直平分线性质求出BD=DC,根据三角形周长求出AB+AC=12cm,根据已知得出AC=AB-2cm,即可求出答案.
试题解析:
∵DE垂直平分BC,
∴BD=CD.
∴△ACD的周长=AD+AC+CD=AD+AC+BD=AB+AC=14cm.
解方程组
得
∴AC=6cm,AB=8cm. 在两个直角三角形中,若有一对角(非直角)相等,一对边相等,则两个直角三角形( )
A. 一定全等 B. 一定不全等 C. 不一定全等 D. 以上都不是
 C
【解析】如果有一对角(非直角)对应相等,一对边对应相等,题中还隐含着一对直角相等,则这两个三角形一定全等,
若不是对应相等,则不一定全等,
故选C.
C
【解析】如果有一对角(非直角)对应相等,一对边对应相等,题中还隐含着一对直角相等,则这两个三角形一定全等,
若不是对应相等,则不一定全等,
故选C. 如图,AB∥CD,HP平分∠DHF,若∠AGH=80°,求∠DHP的度数.
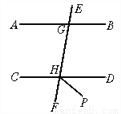
 50°
【解析】试题分析:已知AB∥CD,联系平行线的性质不难得到∠EHD的大小,那么∠FHD的大小也就出来了;观察图形,利用角平分线的性质,即可得到∠DHP的大小.
【解析】
∵AB∥CD,
∴∠CHF=∠AGH=80°,
∴∠DHF=180°-80°=100°.
又∵HP平分∠DHF,
∴∠DHP=∠DHF=50°.
50°
【解析】试题分析:已知AB∥CD,联系平行线的性质不难得到∠EHD的大小,那么∠FHD的大小也就出来了;观察图形,利用角平分线的性质,即可得到∠DHP的大小.
【解析】
∵AB∥CD,
∴∠CHF=∠AGH=80°,
∴∠DHF=180°-80°=100°.
又∵HP平分∠DHF,
∴∠DHP=∠DHF=50°. 
