题目内容
如图，(1)∵∠A=_____(已知)，
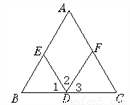
∴AC∥ED( )
(2)∵∠2=_____(已知)，
∴AC∥ED( )
(3)∵∠A+_____=180°(已知)，
∴AB∥FD( )
(4)∵AB∥_____(已知)，
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知)，
∴∠C=∠1( )
(1)∠BED 同位角相等,两直线平行?
(2)∠DFC 内错角相等，两直线平行?
(3)∠AFD 同旁内角互补，两直线平行?
(4)DF 两直线平行，同旁内角互补?
(5)ED 两直线平行，同位角相等
【解析】(1)∠BED ,同位角相等,两直线平行?
(2)∠DFC ,内错角相等，两直线平行?
(3)∠AFD ,同旁内角互补，两直线平行?
(4)...
阅读快车系列答案如图所示,AB-AC=2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,
求AB和AC的长.
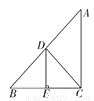
AB=8,AC=6
【解析】试题分析：根据线段垂直平分线性质求出BD=DC，根据三角形周长求出AB+AC=12cm，根据已知得出AC=AB-2cm，即可求出答案．
试题解析：
∵DE垂直平分BC,
∴BD=CD.
∴△ACD的周长=AD+AC+CD=AD+AC+BD=AB+AC=14cm.
解方程组
得
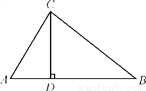
∴AC=6cm，AB=8cm. 如图，在△ABC中，CD⊥AB，垂足为点D.若AB＝12，CD＝6，tanA＝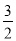
，求sinB＋cosB的值．
.
【解析】试题分析：先在Rt△ACD中，由正切函数的定义得tanA==，求出AD=4，则BD=AB﹣AD=8，再解Rt△BCD，由勾股定理得BC==10，sinB==，cosB==，由此求出sinB+cosB=．
【解析】
在Rt△ACD中，∵∠ADC=90°，
∴tanA===，
∴AD=4，
∴BD=AB﹣AD=12﹣4=8．
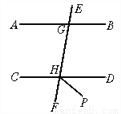
在Rt△BCD中，∵∠BD... 如图，AB∥CD，HP平分∠DHF，若∠AGH=80°，求∠DHP的度数.
50°
【解析】试题分析：已知AB∥CD，联系平行线的性质不难得到∠EHD的大小，那么∠FHD的大小也就出来了；观察图形，利用角平分线的性质，即可得到∠DHP的大小.
【解析】
∵AB∥CD，
∴∠CHF=∠AGH=80°，
∴∠DHF=180°-80°=100°.
又∵HP平分∠DHF，
∴∠DHP=∠DHF=50°. 如图，∠1＝∠B，且∠2＝∠C，则下列结论不成立的是（ ）
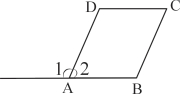
A、AD∥BC B、∠B＝∠C C、∠2＋∠B＝180° D、AB∥CD
B
【解析】
试题分析：由∠1＝∠B可得AD∥BC，再结合∠2＝∠C可得AB∥CD，再依次分析各选项即可作出判断.
∵∠1＝∠B
∴AD∥BC
∴∠2+∠B＝180°
∵∠2＝∠C
∴∠B+∠C＝180°
∴AB∥CD
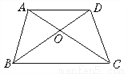
故选B. 如图，AD∥BC，AC与BD相交于O，则图中相等的角有_____对.
四
【解析】∵∠AOB与∠COD是对顶角，∠AOD与∠BOC是对顶角，
∴∠AOB=∠COD，∠AOD=∠BOC.
∵AD∥BC,
∴∠CAD=∠ACB，∠ADB=∠CBD.
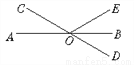
∴图中相等的角有四对. 如图，直线AB、CD相交于点O，OB平分∠DOE，若∠DOE=60°，则∠AOC的度数是_____.
30°
【解析】因为∠BOD=45°，所以∠AOC=∠BOD=45°（对顶角相等），因为OE⊥AB，∴∠AOE=90°，所以∠COE=∠COA+∠AOE=45°+90°=135°. 先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
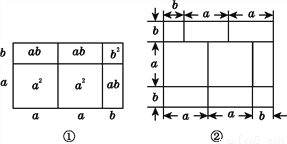
(1)(2a+b)(a+2b)=2a2+5ab+2b2(2)图形见解析
【解析】试题分析：（1）根据所给的长方形面积的两种表示法即可得等式；（2）画一个长为x+p，宽为x+q的长方形即可．
试题解析：
(1)(2a+b)(a+2b)=2a2+5ab+2b2
(2)如图.(所画图形不唯一) 对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C.