题目内容
9.若函数y=x2-2ax+3(0<x<3)的图象恒在x轴上方,则实数a的取值范围是a≤$\sqrt{3}$.分析 由于二次项系数大于0,所以开口向上,分别求出x=0和x=3时,y=3和y=12-6a,由于函数y=x2-2ax+3(0<x<3)的图象恒在x轴上方,所以3(12-6a)≥0,从而求出a的范围.
解答 解:由题意可知:对称轴为x=a,
x=0时,y=3,x=a时,y=12-6a
当a≤0时,
此时函数y的图象恒在x轴上方,
当0<a<3时,函数y的图象恒在x轴上方,
此时△=4a2-12<0,
∴-$\sqrt{3}$<a<$\sqrt{3}$,
∴0<a<$\sqrt{3}$,
当a≥3时,函数y的图象恒在x轴上方,
此时12-6a>0,
∴a<2不符合题意
由于函数y=x2-2ax+3(0<x<3)的图象恒在x轴上方,
综上所述,a$<\sqrt{3}$
故答案为:a<$\sqrt{3}$
点评 本题考查抛物线与x轴的交点,解题的关键是分别求出x=0和x=3时的函数值,然后列出不等式即可求出a的范围,本题属于中等题型.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
14.若-1<x<2,则$\sqrt{4-4x+{x}^{2}}$+$\sqrt{{x}^{2}+2x+1}$化简的结果( )
| A. | 2x-1 | B. | -2x+1 | C. | 3 | D. | -3 |
18.近几年,我国经济高速发展,但退休人员待遇持续偏低.为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工李师傅2014年月退休金为2500元,2016年达到3160元.设李师傅的月退休金从2014年到2016年年平均增长率为x,则可列方程为( )
| A. | 2500(1-x)2=3160 | B. | 2500(1+x)2=3160 | ||
| C. | 3160(1-x)2=2500 | D. | 2500+2500(1+x)+2500(1+x)2=3160 |
19.下列运算正确的是( )
| A. | (ab)5=ab5 | B. | a8÷a2=a6 | C. | (a2)3=a5 | D. | (a-b)5=a5-b5 |
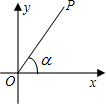 如图,点P到坐标原点O的距离OP=6,线段OP与x轴正半轴的夹角为α,且cosα=$\frac{2}{3}$,则点P的坐标为(4,2$\sqrt{5}$).
如图,点P到坐标原点O的距离OP=6,线段OP与x轴正半轴的夹角为α,且cosα=$\frac{2}{3}$,则点P的坐标为(4,2$\sqrt{5}$). 如图,己知∠1=∠2,要判定△ABD≌△ACD,则需要补充的一个条件为BD=CD.
如图,己知∠1=∠2,要判定△ABD≌△ACD,则需要补充的一个条件为BD=CD. (1)在直角坐标系中画出二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{2}$的图象.
(1)在直角坐标系中画出二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{2}$的图象.