题目内容
1. (1)在直角坐标系中画出二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{2}$的图象.
(1)在直角坐标系中画出二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{2}$的图象.(2)若将y=$\frac{1}{2}$x2-x-$\frac{3}{2}$图象沿x轴向左平移2个单位,请写出平移后图象所对应的函数关系式.
(3)根据图象,写出当y>0时,x的取值范围.
分析 (1)根据抛物线的对称轴,与坐标轴的交点坐标即可大致画出图象.
(2)先将抛物线化为顶点式后,由于沿x轴向左平移2个单位,从而列出函数式.
(3)求出抛物线与x轴的两个交点坐标即可求出y>0,x的取值范围.
解答 解:(1)如图所示
(2) y=$\frac{1}{2}$(x-1)2-2
y=$\frac{1}{2}$(x-1)2-2
将y=$\frac{1}{2}$x2-x-$\frac{3}{2}$图象沿x轴向左平移2个单位,
∴y=$\frac{1}{2}$(x-1+2)2-2=$\frac{1}{2}$x2+x-$\frac{3}{2}$
(3)令y=0代入y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
∴0=$\frac{1}{2}$x2-x-$\frac{3}{2}$
∴x=-1或x=3,
∴当y>0时,
x<-1或x>3
点评 本题考查二次函数的图象与性质,解题的关键是会根据抛物线的解析式求出抛物线的对称轴以及与坐标轴的交点坐标,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.合并同类项2a2b-2ab2-a2b,结果正确的是( )
| A. | 0 | B. | -a2b | C. | -1 | D. | a2b-2ab2 |
12.下列说法正确的是( )
| A. | 平方等于它本身的数是0 | B. | 立方等于它本身的数是±1 | ||
| C. | 绝对值等于它本身的数是正数 | D. | 倒数等于它本身的数是±1 |
10.下列说法正确的是( )
| A. | 经过一点可以作两条直线 | B. | 棱柱侧面的形状可能是一个三角形 | ||
| C. | 连接两点的线段叫两点间的距离 | D. | 棱柱的每条棱长都相等 |
10.下列各数:5.9、-2$\frac{1}{3}$、-7、0、$\frac{12}{5}$、8中,正分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 已知:如图,△ABC是直角三角形,∠C=90°,∠A=30°.求证:BC=$\frac{1}{2}$AB.
已知:如图,△ABC是直角三角形,∠C=90°,∠A=30°.求证:BC=$\frac{1}{2}$AB.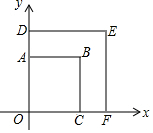 如图,正方形ODEF与正方形OABC是位似图形,点O为位似中心,相似比为2:$\sqrt{2}$,点D的坐标为(0,2$\sqrt{2}$),则点B的坐标是(2,2).
如图,正方形ODEF与正方形OABC是位似图形,点O为位似中心,相似比为2:$\sqrt{2}$,点D的坐标为(0,2$\sqrt{2}$),则点B的坐标是(2,2).