题目内容
19.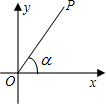 如图,点P到坐标原点O的距离OP=6,线段OP与x轴正半轴的夹角为α,且cosα=$\frac{2}{3}$,则点P的坐标为(4,2$\sqrt{5}$).
如图,点P到坐标原点O的距离OP=6,线段OP与x轴正半轴的夹角为α,且cosα=$\frac{2}{3}$,则点P的坐标为(4,2$\sqrt{5}$).
分析 过点P作PA⊥x,垂足为A,由cosA、OP可求出P点的横坐标OA,再由勾股定理求出P点的纵坐标PA.
解答  解:过点P作PA⊥x,垂足为A.
解:过点P作PA⊥x,垂足为A.
∵cosA=$\frac{OA}{OP}=\frac{2}{3}$,OP=6,
∴0A=4.
在Rt△OPA中,
PA=$\sqrt{{OP}^{2}-{0A}^{2}}$
=2$\sqrt{5}$.
所以点P的坐标为(4,2$\sqrt{5}$)
故答案为:(4,2$\sqrt{5}$)
点评 本题主要考察了解直角三角形的相关定义.理解余弦的意义构造直角三角形是解决本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
7.在Rt△ABC中,∠C=90°,a=1,b=$\sqrt{3}$,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
14.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为( )
| A. | π | B. | 1 | C. | $\frac{2}{3}$π | D. | 2 |
11.合并同类项2a2b-2ab2-a2b,结果正确的是( )
| A. | 0 | B. | -a2b | C. | -1 | D. | a2b-2ab2 |