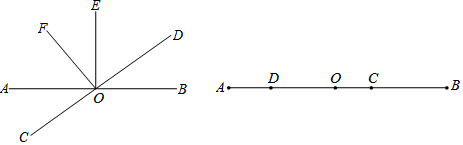题目内容

20．如图，己知∠1=∠2，要判定△ABD≌△ACD，则需要补充的一个条件为BD=CD．

分析 此题是一道开放型的题目，答案不唯一，只要添加一个条件，符合全等三角形的判定定理即可．

解答 解：BD=CD，
理由是：∵在△ABD和△ACD中
$\left\{\begin{array}{l}{BD=CD}\\{∠1=∠2}\\{AD=AD}\end{array}\right.$
∴△ABD≌△ACD（SAS），
故答案为：BD=CD．

点评 本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键．

练习册系列答案
相关题目
10．（1）如图1，直线AB，CD相交于点O，OE⊥AB，OF⊥CD．
①直接写出图中∠AOF的余角；
②如果∠EOF=$\frac{1}{5}$∠AOD，求∠EOF的度数．
（2）如图2，已知O为线段AB中点，AC=$\frac{2}{3}$AB，BD=$\frac{4}{5}$AB，线段OC长为1，求线段AB，CD的长．
11．合并同类项2a2b-2ab2-a2b，结果正确的是（　　）
A．0B．-a2bC．-1D．a2b-2ab2
8．一次函数y=-2x+b的图象经过点（-2，3），则b=-1．
15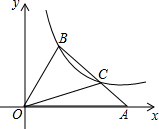．如图，在平面直角坐标系xOy中，△OAB的顶点A在x轴正半轴上，OC是△OAB的中线，点B、C在反比例函数y=$\frac{k}{x}$（x＞0）的图象上，若△OAB的面积等于6，则k的值为（　　）
A．2B．4C．6D．8
5．观察下列各式：$\frac{1}{2}$=$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$，$\frac{1}{6}$=$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，$\frac{1}{12}$=$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$，$\frac{1}{20}$=$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$，$\frac{1}{30}$=$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$，…
（1）请你根据上面各式的规律，写出符合该规律的一道等式：$\frac{1}{42}$=$\frac{1}{6×7}$=$\frac{1}{6}$-$\frac{1}{7}$
（2）请利用上述规律计算：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n（n+1）}$=$\frac{n}{n+1}$
（用含有n的式子表示）
（3）请利用上述规律解方程：$\frac{1}{（x-2）（x-1）}$+$\frac{1}{（x-1）x}$+$\frac{1}{x（x+1）}$=$\frac{1}{x+1}$．
12．下列说法正确的是（　　）
A．平方等于它本身的数是0B．立方等于它本身的数是±1
C．绝对值等于它本身的数是正数D．倒数等于它本身的数是±1
9．若函数y=x2-2ax+3（0＜x＜3）的图象恒在x轴上方，则实数a的取值范围是a≤$\sqrt{3}$．
10．下列说法正确的是（　　）
A．经过一点可以作两条直线B．棱柱侧面的形状可能是一个三角形
C．连接两点的线段叫两点间的距离D．棱柱的每条棱长都相等

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网