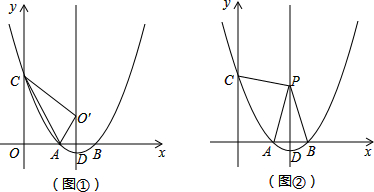题目内容
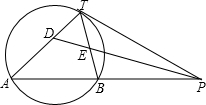 如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=
如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=| 3 |
| TE |
| AD |
考点:切线的性质
专题:
分析:首先直接运用切割线定理求出PA的长;运用切线的性质定理及角平分线的定义,结合三角形外角的性质证明TD=TE;运用三角形内角平分线的性质即可解决问题.
解答: 解:∵PT是⊙O的切线,直线PA与⊙O交于A、B两点,
解:∵PT是⊙O的切线,直线PA与⊙O交于A、B两点,
∴PT2=PA•PB,
而PT=2,PB=
,
∴PA=
=
;
∵PT是⊙O的切线,
∴∠PTB=∠A;
又∵∠TPA的平分线分别交直线TA、TB于D、E两点,
∴∠TPE=∠APD,
∴∠PTB+∠TPE=∠A+∠APD;
∵∠TDE=∠A+∠APD,∠TED=∠PTB+∠TPE
∴∠TDE=∠TED,
∴TD=TE;
∵PD平分∠TPA,
∴
=
=
=
,
=
,
故答案为:
,
.
 解:∵PT是⊙O的切线,直线PA与⊙O交于A、B两点,
解:∵PT是⊙O的切线,直线PA与⊙O交于A、B两点,∴PT2=PA•PB,
而PT=2,PB=
| 3 |
∴PA=
| 4 | ||
|
4
| ||
| 3 |
∵PT是⊙O的切线,
∴∠PTB=∠A;
又∵∠TPA的平分线分别交直线TA、TB于D、E两点,
∴∠TPE=∠APD,
∴∠PTB+∠TPE=∠A+∠APD;
∵∠TDE=∠A+∠APD,∠TED=∠PTB+∠TPE
∴∠TDE=∠TED,
∴TD=TE;
∵PD平分∠TPA,
∴
| TD |
| AD |
| PT |
| PA |
| 2 | ||||
|
3
| ||
| 4 |
| TE |
| AD |
3
| ||
| 4 |
故答案为:
4
| ||
| 3 |
3
| ||
| 4 |
点评:该题主要考查了圆切线的性质定理及其应用问题;同时还考查了角的平分线的性质及其应用问题;灵活运用有关定理来解题是关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
已知点A(2a+3b,-2)和点B(8,2a+4b)关于原点对称,那么a+b的值为( )
| A、6 | B、10 | C、-9 | D、-16 |
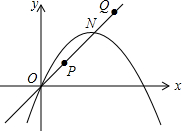 已知抛物线y=-
已知抛物线y=- 如图,正方形ABCD中,连接BD.点E在边BC上,且CE=2BE.连接AE交BD于F;连接DE,取BD的中点O;取DE的中点G,连接OG.下列结论:
如图,正方形ABCD中,连接BD.点E在边BC上,且CE=2BE.连接AE交BD于F;连接DE,取BD的中点O;取DE的中点G,连接OG.下列结论: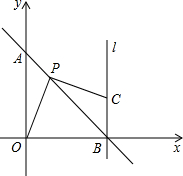 如图,在平面直角坐标系xOy中,A、B的坐标分别是(0,4)、(4,0).
如图,在平面直角坐标系xOy中,A、B的坐标分别是(0,4)、(4,0).