题目内容
解方程或计算
(1)2x2-2x-1=0;
(2)(2y+1)2+3(2y+1)+2=0;
(3)计算:-12012+(4-π)0-cos45°+(
)-1.
(1)2x2-2x-1=0;
(2)(2y+1)2+3(2y+1)+2=0;
(3)计算:-12012+(4-π)0-cos45°+(
| 2 |
考点:换元法解一元二次方程,实数的运算,零指数幂,负整数指数幂,解一元二次方程-公式法,特殊角的三角函数值
专题:
分析:(1)用一元二次方程的求根公式x=
可求出方程的两根.
(2)用先设2y+1=x,则原方程变形为x2+3x+2=0,运用因式分解法解得x1=-2,x2=-1,再把x1=-2,x2=-1分别代入2y+1=x得到关于y的一元一次方程,然后解两个一元一次方程,最后确定原方程的解.
(3)分别计算出-12012,(4+π)0,cos45°,(
)-1的值,然后合并同类项即可.
-b±
| ||
| 2a |
(2)用先设2y+1=x,则原方程变形为x2+3x+2=0,运用因式分解法解得x1=-2,x2=-1,再把x1=-2,x2=-1分别代入2y+1=x得到关于y的一元一次方程,然后解两个一元一次方程,最后确定原方程的解.
(3)分别计算出-12012,(4+π)0,cos45°,(
| 2 |
解答:解:(1)2x2-2x-1=0;
解:a=2,b=-2,c=-1,
b2-4ac=4-4×2×(-1)
=4+8
=12;
∴x=
=
=1±
,
∴x1=1+
,x2=1-
.
(2)(2y+1)2+3(2y+1)+2=0;
设2y+1=x,则原式变形为:
x2+3x+2=0;
分解因式,得(x+2)(x+1)=0,
∴x1=-2,x2=-1,
当2y+1=-2时,y1=-
,
当2y+1=-1时,y2=-1,
所以原方程的解为x1=-
,x2=-1.
(3)计算:-12012+(4-π)0-cos45°+(
)-1.
=-1+1-
+
=0.
解:a=2,b=-2,c=-1,
b2-4ac=4-4×2×(-1)
=4+8
=12;
∴x=
-b±
| ||
| 2a |
2±
| ||
| 2 |
| 3 |
∴x1=1+
| 3 |
| 3 |
(2)(2y+1)2+3(2y+1)+2=0;
设2y+1=x,则原式变形为:
x2+3x+2=0;
分解因式,得(x+2)(x+1)=0,
∴x1=-2,x2=-1,
当2y+1=-2时,y1=-
| 3 |
| 2 |
当2y+1=-1时,y2=-1,
所以原方程的解为x1=-
| 3 |
| 2 |
(3)计算:-12012+(4-π)0-cos45°+(
| 2 |
=-1+1-
| ||
| 2 |
| ||
| 2 |
=0.
点评:本题考查了解一元二次方程的方法以及实数的运算;解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法,并且注意零指数幂、负整数指数幂、特殊角的三角函数的计算.

练习册系列答案
相关题目
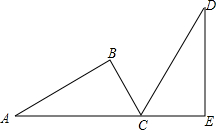 如图,在△ABC中,∠ACB=90°,∠A=30°,把△ABC绕点C旋转一定角度后得到△DEC,点A、C、E在同一直线上,则这个旋转角度为( )
如图,在△ABC中,∠ACB=90°,∠A=30°,把△ABC绕点C旋转一定角度后得到△DEC,点A、C、E在同一直线上,则这个旋转角度为( )| A、60° | B、90° |
| C、120° | D、150° |
一个点从数轴上的原点开始,先向右移动4个单位长度,再向左移动5个单位长度,则此时这个点表示的数是( )
| A、0 | B、-2 | C、+1 | D、-1 |
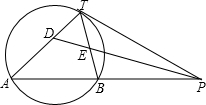 如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=
如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=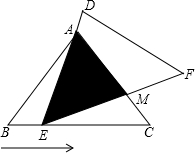 在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.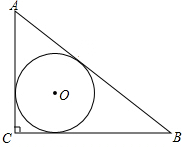 如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为5,4,3,求△ABC的内切圆的半径r.
如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为5,4,3,求△ABC的内切圆的半径r. 如图,在3×3的方格网中,连接AB、BC、CA,请观察并度量∠1、∠2、…、∠6,然后回答下列问题:
如图,在3×3的方格网中,连接AB、BC、CA,请观察并度量∠1、∠2、…、∠6,然后回答下列问题: