题目内容
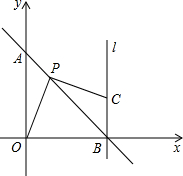 如图,在平面直角坐标系xOy中,A、B的坐标分别是(0,4)、(4,0).
如图,在平面直角坐标系xOy中,A、B的坐标分别是(0,4)、(4,0).(1)若P为AB的中点,求P点的坐标;
(2)若P为线段AB上异于A、B的任意一点,CP⊥OP,下列结论:
①CP+OP为定值;
②CP:OP为定值.
其中只有一个是正确的,请你判断出正确的结论,并证明正确的结论,以及求出它的值.
考点:一次函数综合题
专题:综合题
分析:(1)由P为AB中点,根据A与B的坐标,利用中点坐标公式求出P的坐标即可;
(2)正确结论为:②CP:OP为定值,这个定值为1,理由为:作PK⊥OB,垂足为K;PN⊥OA,垂足为N,NP的延长线交直线l于M,易证:四边形MNOB,MPKB,PNOK都是矩形,利用两对角相等的三角形相似,得到三角形NPO与三角形CMP相似,由相似得比例列出关系式,根据三角形AOB为等腰直角三角形得到三角形PKB为等腰直角三角形,得到PK=KB,代入比例式变形即可得到结果.
(2)正确结论为:②CP:OP为定值,这个定值为1,理由为:作PK⊥OB,垂足为K;PN⊥OA,垂足为N,NP的延长线交直线l于M,易证:四边形MNOB,MPKB,PNOK都是矩形,利用两对角相等的三角形相似,得到三角形NPO与三角形CMP相似,由相似得比例列出关系式,根据三角形AOB为等腰直角三角形得到三角形PKB为等腰直角三角形,得到PK=KB,代入比例式变形即可得到结果.
解答: 解:(1)若P为AB的中点,则有P(2,2);
解:(1)若P为AB的中点,则有P(2,2);
(2)正确结论为:②CP:OP为定值,这个定值为1,理由如下:
作PK⊥OB,垂足为K;PN⊥OA,垂足为N,NP的延长线交直线l于M,
易证:四边形MNOB,MPKB,PNOK都是矩形,
∵OP⊥PC,
∴∠OPC=90°,
∴∠NPO+∠MPC=90°,
∵∠NPO+∠NOP=90°,
∴∠NOP=∠MPC,
∵∠ONP=∠PMC=90°,
∴△NPO∽△CMP,
∴CP:PO=PM:ON,
∵PK=ON,PM=KB,OA=OB,
∴△AOB为等腰直角三角形,即∠OBA=45°,
∵∠PKB=90°,
∴△PKB为等腰直角三角形,即∠KPB=45°=∠KBP,
∴PK=KB,
∴CP:PO=PK:KB=1,
∴CP:PO=1.
 解:(1)若P为AB的中点,则有P(2,2);
解:(1)若P为AB的中点,则有P(2,2);(2)正确结论为:②CP:OP为定值,这个定值为1,理由如下:
作PK⊥OB,垂足为K;PN⊥OA,垂足为N,NP的延长线交直线l于M,
易证:四边形MNOB,MPKB,PNOK都是矩形,
∵OP⊥PC,
∴∠OPC=90°,
∴∠NPO+∠MPC=90°,
∵∠NPO+∠NOP=90°,
∴∠NOP=∠MPC,
∵∠ONP=∠PMC=90°,
∴△NPO∽△CMP,
∴CP:PO=PM:ON,
∵PK=ON,PM=KB,OA=OB,
∴△AOB为等腰直角三角形,即∠OBA=45°,
∵∠PKB=90°,
∴△PKB为等腰直角三角形,即∠KPB=45°=∠KBP,
∴PK=KB,
∴CP:PO=PK:KB=1,
∴CP:PO=1.
点评:此题属于一次函数综合题,涉及的知识有:相似三角形的判定与性质,等腰直角三角形的判定与性质,以及矩形的判定与性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
一个点从数轴上的原点开始,先向右移动4个单位长度,再向左移动5个单位长度,则此时这个点表示的数是( )
| A、0 | B、-2 | C、+1 | D、-1 |
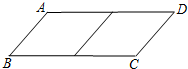 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.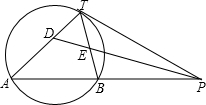 如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=
如图,PT是⊙O的切线,切点为T,直线PA与⊙O交于A、B两点,∠TPA的平分线分别交直线TA、TB于D、E两点.已知PT=2,PB=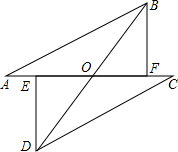 已知如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于点F,DE⊥AC于点E,AE=CF,求证:BD与EF互相平分.
已知如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于点F,DE⊥AC于点E,AE=CF,求证:BD与EF互相平分.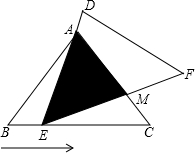 在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.